Analysis

1 Packages

library(tidyverse)
library(metan)
library(rio)
library(ggrepel)
library(R2OpenBUGS)
library(boa)
library(ggformula)

To perform the bayesian analysis, the Open BUGS software need to be installed. Follow these instructions to install it.

2 Data

data_cv <-  
  import("http://bit.ly/data_cvs") %>% 
  select(GY:NGS)

# Long format
data_cv_long <-
data_cv %>%
  pivot_longer(everything(), 
               names_to = "var",
               values_to = "cv") %>%
  remove_rows_na()

# samples per variable
data_cv_long %>% n_by(var)

# create a list of variables with no missing values
df <- lapply(data_cv, remove_rows_na)

3 Bayesian

3.1 Function

bayes <- function(df){
linemodel <- function(){
  for (i in 1:64) # change the number of samples for each variable
  {
    y[i] ~ dgamma(r, mu)
  }  
  r ~ dunif(0,5)
  mu ~ dunif(0,5)    
}
################ Especificando os dados
linedata <- list(y = df[[1]])
###################### Specification innitial values
lineinits <- function(){list(r = 0.5, mu = 1) }
#Specification the parameters
parameters <- c("r","mu")
############# Execution function analysis with bugs package of R2OpenBUGS
Niter <- 10000
Nburn <- 1000
Nthin <- 10
################ results of descriptive statistics #############
modelo <- bugs(data = linedata,
               inits = lineinits,
               parameters.to.save = parameters,
               model.file = linemodel,
               n.chains = 1,
               n.iter = Niter,
               n.burnin = Nburn,
               n.thin = Nthin,
               debug = TRUE)
return(modelo$sims.matrix[,1] / modelo$sims.matrix[,2])
}

3.2 Posterior distribution

GY <- bayes(df$GY)
GYP <- bayes(df$GYP)
HGW <- bayes(df$HGW)
TGW <- bayes(df$TGW)
HW <- bayes(df$HW)
DF <- bayes(df$DF)
PH <- bayes(df$PH)
LS <- bayes(df$LS)
NSPS <- bayes(df$NSps)
NGS <- bayes(df$NGS)

3.3 Credibility intervals and mean posterior for each trait

posterior <- import("http://bit.ly/data_posterior")
conf_int_bayes <- 
sapply(posterior, 
       function(x){
         conf_int <- boa.hpd(x, 0.05)
         data.frame(LCI = conf_int[[1]],
                    MEAN = mean(x),
                    UCI = conf_int[[2]])
       }) %>% 
  t()

3.4 Marginal posterior density

posterior_long <- posterior %>% pivot_longer(everything())


ggplot(posterior_long, aes(value))+
  geom_density(fill = "red", alpha = 0.5, size = 0.1) +
  theme(panel.grid.minor = element_blank(),
        legend.position = "bottom",
        legend.title = element_blank(),
        axis.text = element_text(color = "black"),
        axis.ticks = element_line(color = "black"),
        axis.ticks.length = unit(0.15, "cm")) +
  facet_wrap(~ name, scales = "free_y", ncol = 5) +
  theme(panel.grid.minor = element_blank(),
        legend.position = "bottom",
        legend.title = element_blank(),
        axis.text = element_text(color = "black"),
        axis.ticks = element_line(color = "black"),
        axis.ticks.length = unit(0.15, "cm")) +
  labs(x = "Coefficient of variation (%)",
       y = "Density")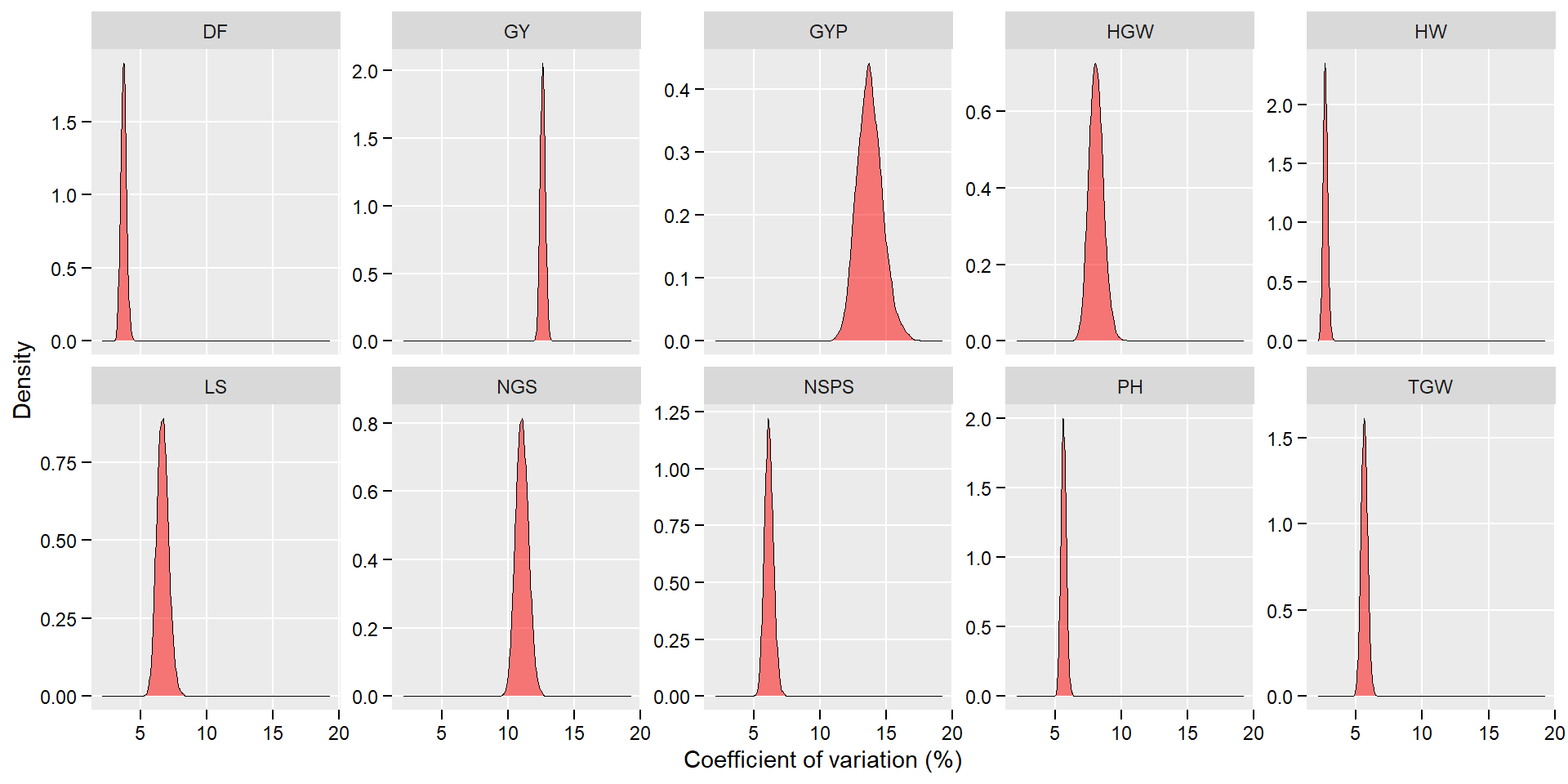

ggsave("figs/fig1_posterior.jpg", dpi = 600, width = 25, height = 10, units = "cm")


# An alternative plot
ggplot(posterior_long, aes(value))+
  geom_density(aes(fill = name),
               alpha = 0.5) +
  theme(panel.grid.minor = element_blank(),
        legend.position = "bottom",
        legend.title = element_blank(),
        axis.text = element_text(color = "black"),
        axis.ticks = element_line(color = "black"),
        axis.ticks.length = unit(0.15, "cm")) +
  theme(panel.grid.minor = element_blank(),
        legend.position = "bottom",
        legend.title = element_blank(),
        axis.text = element_text(color = "black"),
        axis.ticks = element_line(color = "black"),
        axis.ticks.length = unit(0.15, "cm")) +
  labs(x = "Coefficient of variation (%)",
       y = "Density")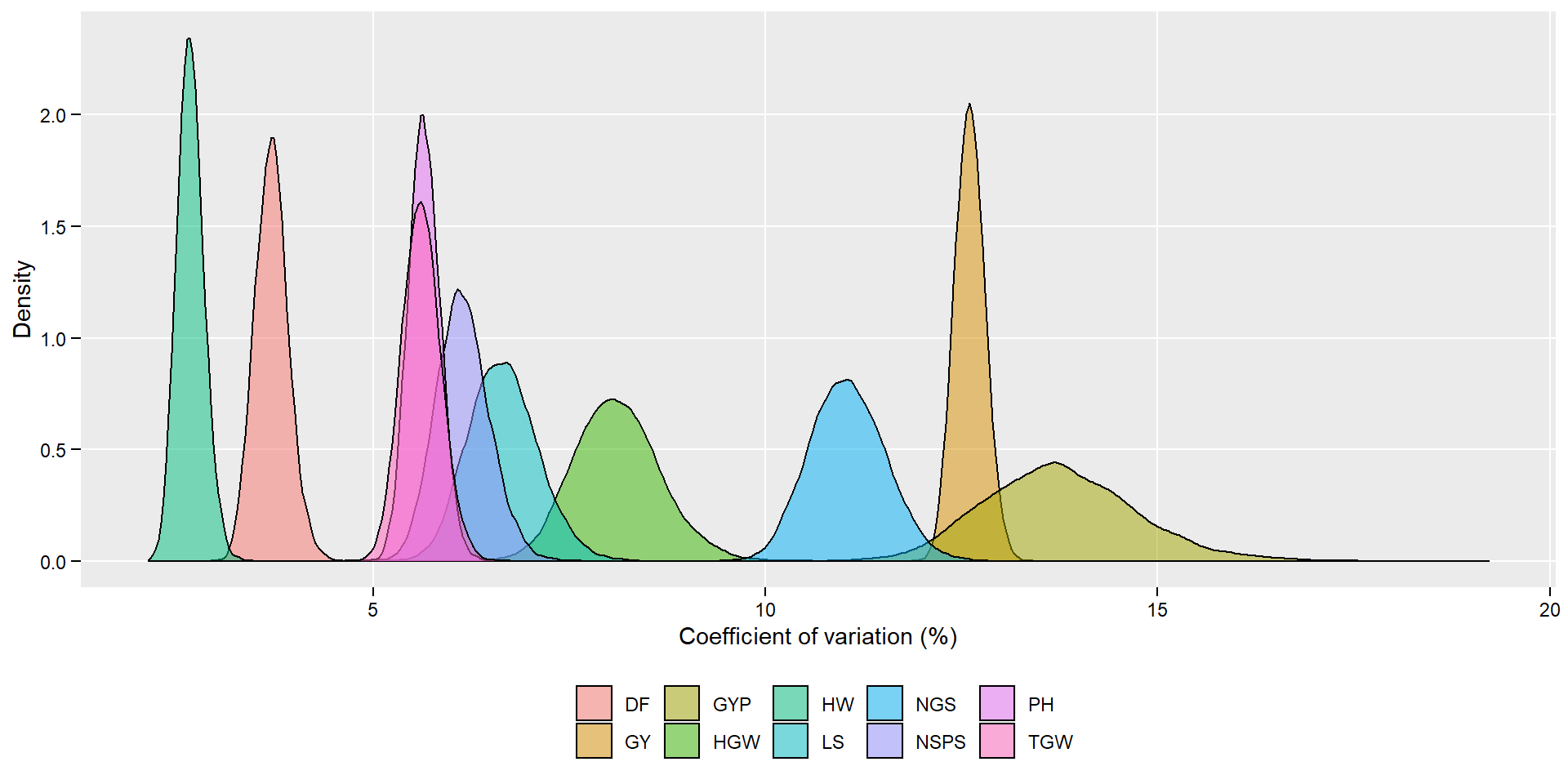

ggsave("figs/fig1_posterior2.jpg", dpi = 600, width = 25, height = 10, units = "cm")

4 Frequentist

4.1 Confidence interval

get_confint <- function(df, var){
    if(is.grouped_df(df)){
      results <- doo(df, get_confint, var = {{var}})
      return(results)
    }
    values <- na.omit(df %>% select_cols({{var}}) %>% pull())
    model <- glm(values ~ 1, family = Gamma(link = "identity"))
    conf <- confint(model)
    MEAN <- coef(model)[[1]]
    LCI <- conf[[1]]
    UCI <-  conf[[2]]
    data.frame(LCI = LCI, MEAN = MEAN, UCI = UCI)
  }

freq_lim <- 
  data_cv_long %>%
    group_by(var) %>% 
    get_confint(cv)

p <-
  gf_density( ~ cv | var,
              data = data_cv_long,
              fill = "red",
              alpha = 0.5) %>%
  gf_fitdistr(linetype = 2) %>%
  gf_fitdistr(dist = "gamma", color = "blue")

p +
  facet_wrap(~var, nrow = 2, scales = "free_y") +
  theme(panel.grid.minor = element_blank(),
        axis.text = element_text(color = "black"),
        axis.ticks = element_line(color = "black"),
        axis.ticks.length = unit(0.15, "cm")) +
  scale_y_continuous(expand = expansion(c(0, 0.05))) +
  labs(x = "Coeficient of variation (%)",
       y = "Density")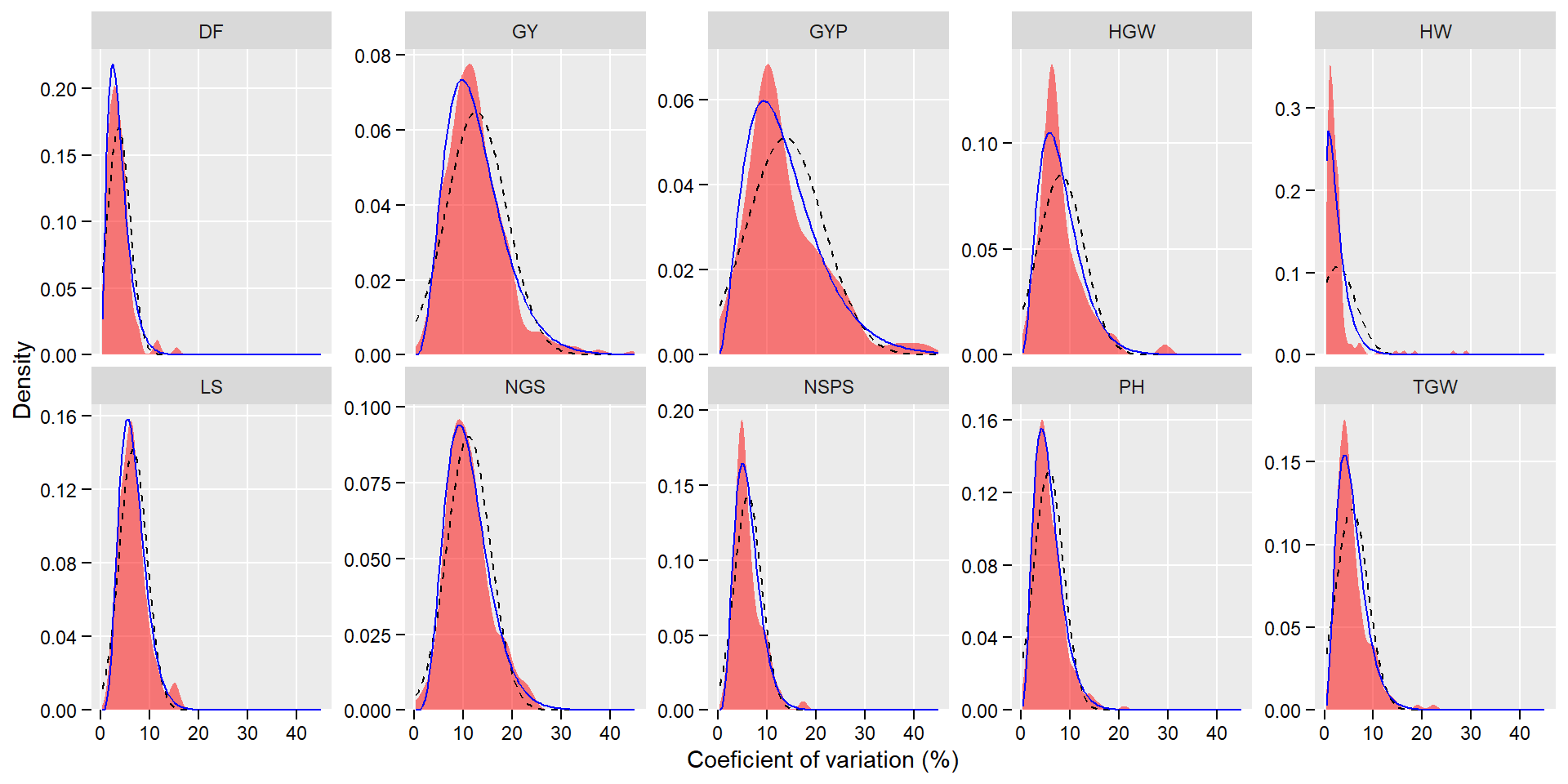

ggsave("figs/fig2_density.jpg", dpi = 600, width = 25, height = 10, units = "cm")

5 Results

5.1 Confidence interval

df_confint <- import("http://bit.ly/data_confint")


ggplot(df_confint, aes(MEAN, fct_rev(VAR), color = APPROACH)) +
  geom_point(position = position_dodge(width = 0.7),
             size = 2) +
  geom_errorbarh(aes(xmin = LCI, xmax = UCI),
                 position = position_dodge(width = 0.7),
                 width = 0.3) +
  scale_x_continuous(breaks = seq(2, 19, by = 2),
                     expand = c(0.15, 0.15)) +
  theme(panel.grid.minor = element_blank(),
        legend.position = "bottom",
        legend.title = element_blank(),
        axis.text = element_text(color = "black"),
        axis.title  = element_text(color = "black"),
        axis.ticks = element_line(color = "black"),
        axis.ticks.length = unit(0.15, "cm")) +
  labs(x = "Coefficient of variation (%)",
       y = "Variable") +
  geom_text(aes(label = round(LCI, 2),
                x = LCI),
            position = position_dodge(width = 0.7), 
            hjust = 1.2,
            size = 2.5,
            show.legend = FALSE) +
  geom_text(aes(label = round(UCI, 2),
                x = UCI),
            position = position_dodge(width = 0.7), 
            hjust = -0.3,
            size = 2.5,
            show.legend = FALSE)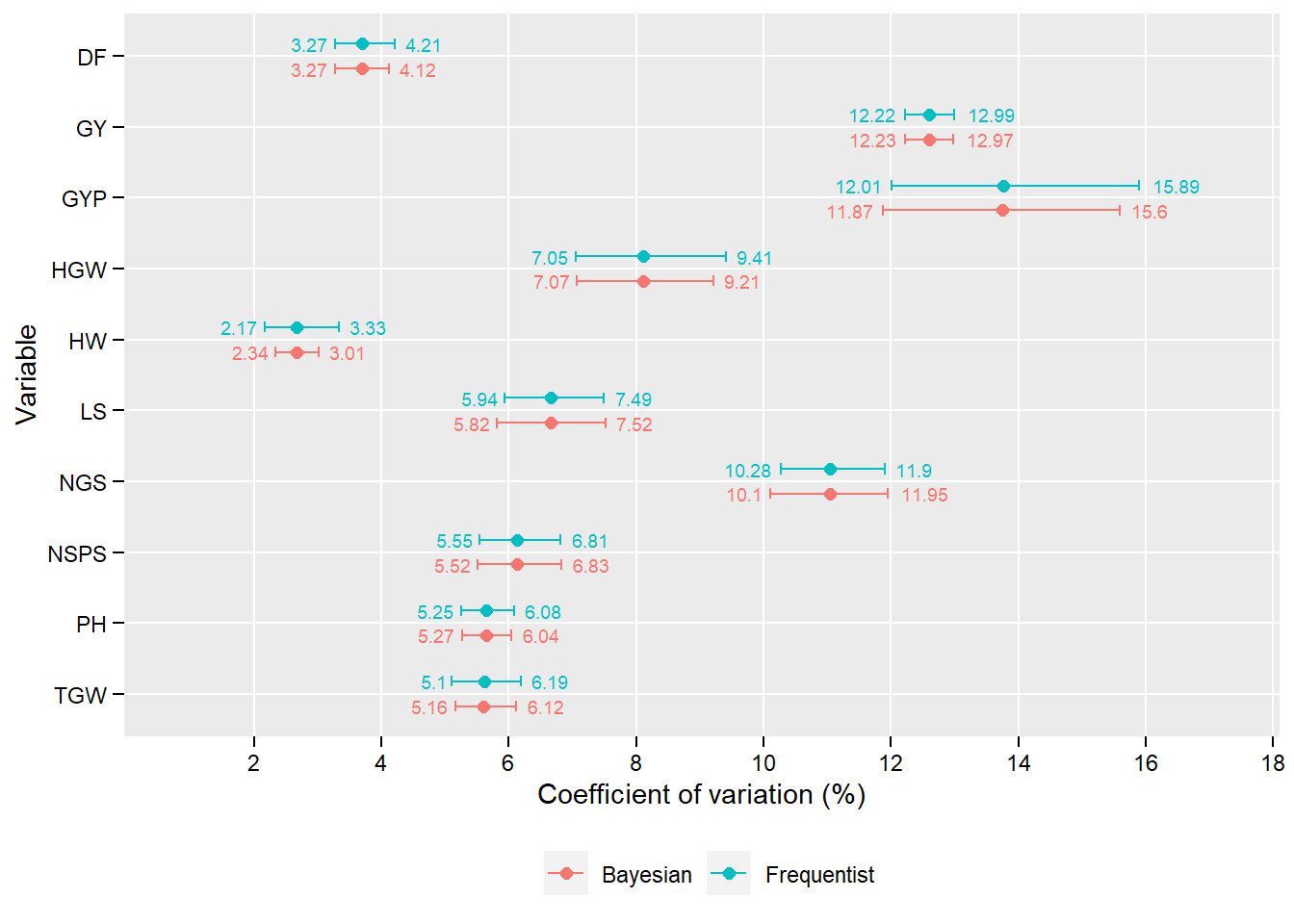

ggsave("figs/fig3_confidence.jpg", dpi = 600, width = 10, height = 12, units = "cm")