library(DiagrammeR)
mermaid("
graph TB
Start -->|0,5|A(1)
Start -->|0,5|B(0)
")3. Distribuições discretas
Introdução à probabilidade
Um modelo probabilístico é um modelo em que, à priori, não é possível definir um resultado particular. Este modelo é especificado por meio de uma distribuição de probabilidade. Geralmente, modelos probabilísticos são utilizados quando se tem um grande número de variáveis influenciando o resultado e estas variáveis não podem ser controladas. Como exemplo, pode-se citar a observação da germinação de uma semente, o lançamento de um dado, onde tenta-se prever o número da face que irá sair, etc.
Distribuição binomial
Seja \(E\) um experimento aleatório e \(\Omega\) um espaço amostra associado, onde \(n\) é o número de vezes que o experimento \(E\) é repetido, \(p\) é a probabilidade de \(\Omega\) ocorrer em cada uma das \(n\) repetições de \(E\). Como existem apenas duas situações (\(\Omega\) ocorre ou \(\Omega\) não ocorre), pode-se determinar a probabilidade de \(\Omega\) não ocorrer como sendo \(q = 1 - p\).
Algumas condições devem ser respeitadas
- São feitas \(n\) repetições do experimento, onde \(n\) é uma constante;
- Há apenas dois resultados possíveis em cada repetição, denominados sucesso e falha
- A probabilidade de sucesso (\(p\)) e de falha \(q\) permanecem constante em todas as repetições;
- As repetições são independentes, ou seja, o resultado de uma repetição não é influenciado por outros resultados.
Se \(X\) é uma variável aleatória com um comportamento Binomial, então a probabilidade de \(X\) assumir um dos valores \(k\) do conjunto \(\Omega\) é calculada por:
\[ P(X = k) = \left( \begin{array}{l}n\\k\end{array} \right) \times {p^k} \times {q^{n - k}} \]
Onde:
- \(p\) é probabilidade de sucesso;
- \(q\) é probabilidade de fracasso;
- \(k\) é número de sucessos;
- \(n\) é tamanho amostral (número de experimentos).
Um exemplo simples
Consideremos a variável aleatória discreta X como o sexo de um bezerro nascido. Denotando sucesso (1 = fêmea) e fracasso (2 = macho), a probabilidade de sucesso é \(p = 0,5\) e a de fracasso \(q = 1 - q = 0,5\). Assim, considerando o parto de uma vaca, há 50% de chance de nascimento de uma terneira.
Considerando duas vacas prenhas, com a mesma probabilidade de nascimento de fêmeas, temos então o seguinte cenário.
flowchart
Start --> |0,5|A(1)
Start --> |0,5|B(0)
A --> |0,5|C(1)
A --> |0,5|D(0)
B --> |0,5|E(1)
B --> |0,5|F(0)
C --> G(11 = pp)
D --> H(10 = pq)
E --> I(01 = qp)
F --> J(00 = qq)
Assim, as probabilidades associadas ao número de nascimentos de bezzeras são dadas por
- Nenhuma bezerra
\[ P(X = 0) = \left( \begin{array}{l}2\\0\end{array} \right) \times {0,5^0} \times {0,5^{2 - 0}} = 0,25 \]
- Uma bezerra
\[ P(X = 1) = \left( \begin{array}{l}2\\1\end{array} \right) \times {0,5^1} \times {0,5^{2 - 1}} = 0,50 \]
- Duas bezerras
\[ P(X = 2) = \left( \begin{array}{l}2\\2\end{array} \right) \times {0,5^2} \times {0,5^{2 - 2}} = 0,25 \]
No software R, a probabilidade de sucesso de um evento para uma variável que segue uma distribuição binomial é computada com a função dbinom().
args(dbinom)function (x, size, prob, log = FALSE)
NULLxé o vetor de quantiles (sucesso);sizeé o número de experimentos (repetições);probé a probabilidade de sucesso em cada experimento aleatório.
library(tibble)
data.frame(nbez = 0:2,
prob = dbinom(0:2, size = 2, prob = 0.5)) nbez prob
1 0 0.25
2 1 0.50
3 2 0.25A mesma lógica é utilizada para uma situação onde três vacas estão prenhas. Assim, \(n = 3\), gera o seguinte cenário.
mermaid("
graph TB
Start --> |0,5|A(1)
Start --> |0,5|B(0)
A --> |0,5|C(1)
A --> |0,5|D(0)
B --> |0,5|E(1)
B --> |0,5|F(0)
C --> |0,5|G(1)
C --> |0,5|H(0)
D --> |0,5|I(1)
D --> |0,5|J(0)
E --> |0,5|K(1)
E --> |0,5|L(0)
F --> |0,5|M(1)
F --> |0,5|N(0)
G --> O(111 = ppp)
H --> P(110 = ppq)
I --> Q(101 = pqp)
J --> R(100 = pqq)
K --> S(011 = qpp)
L --> T(010 = qpq)
M --> U(001 = qqp)
N --> V(000 = qqq)
")data.frame(n_femeas = 0:3,
prob = dbinom(0:3, size = 3, prob = 0.5)) n_femeas prob
1 0 0.125
2 1 0.375
3 2 0.375
4 3 0.125Exercício bezerro
Um produtor possui quatro vacas prenhas de monta natural. Como está cursando a disciplina de Bioestatística, ele gostaria de calcular probabilidades associadas ao nascimento de bezerras fêmeas.
library(tibble)
bezerros <-
tibble(nbez = 0:4,
prob = dbinom(x = 0:4, size = 4, prob = 0.5),
prob_ac = cumsum(prob),
prob_ac_inv = rev(prob_ac))
bezerros# A tibble: 5 × 4
nbez prob prob_ac prob_ac_inv
<int> <dbl> <dbl> <dbl>
1 0 0.0625 0.0625 1
2 1 0.25 0.313 0.938
3 2 0.375 0.688 0.688
4 3 0.25 0.938 0.313
5 4 0.0625 1 0.0625# Gráfico da distribuição
library(tidyverse)
ggplot(bezerros, aes(nbez, prob))+
geom_bar(stat = "identity",
col = "black",
size = 0,
fill = "cyan")+
labs(x = "Número de bezerros fêmeas",
y = "Probabilidade")+
scale_y_continuous(expand = expansion(mult = c(0, 0.1))) +
scale_x_continuous(expand = expansion(mult = c(0, 0))) +
theme_grey(base_size = 14) +
theme(panel.grid.minor = element_blank())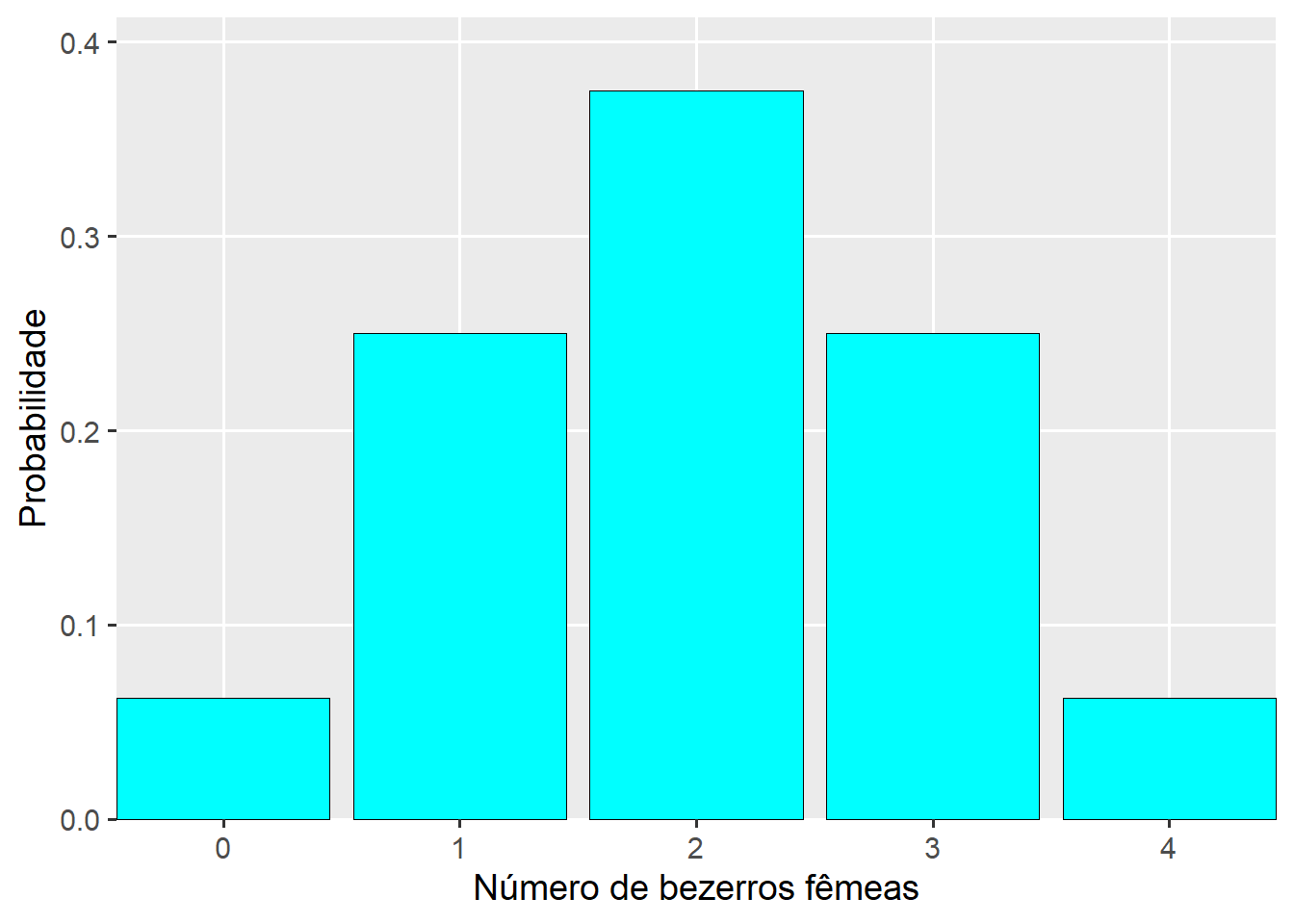
Exercício questões prova
Considere uma prova de estatística com peso 10 contendo 10 questões, cada uma com 5 alternativas. Apenas 1 é correta. Se o aluno tirar uma nota inferior a 4, o aluno está reprovado. Notas entre 4 e 7 fazem com que o aluno fique em exame. Se a nota for superior a 7 o aluno passa. Como João não prestou atenção nas aulas de estatística, ele decidiu “chutar” todas as questões. Calcule as probabilidades que se pede.
Probabilidade de não acertar nenhuma questão
dbinom(x = 0, size = 10, prob = 0.2)[1] 0.1073742Probabilidade de ser reprovado
João será reprovado caso acerte menos que quatro questões. Logo, a soma as probabilidades de acertar 0, 1, 2 e 3 questões é esta probabilidade.
dbinom(x = 0:3, size = 10, prob = 0.2) %>% sum()[1] 0.8791261Probabilidade de ficar em exame
João ficará em exame caso acerte entre 4 e 7 questões. Logo, a probabilidade de ficar em exame será a soma das probabilidades individuais destes números de questões.
dbinom(x = 4:7, size = 10, prob = 0.2) %>% sum()[1] 0.120796Passe na prova
João somente passará na prova, caso acerte mais que sete questões. Valendo-se da propriedade da soma das probabilidades, a probabilidade de João passar na prova é data tanto somando-se as probabilidades de acertar 8, 9 e 10 questões, quanto subtraindo a unidade da probabilidade da soma de acerto de até 7 questões.
dbinom(x = 8:10, size = 10, prob = 0.2) %>% sum()[1] 7.79264e-051 - dbinom(0:7, size = 10, prob = 0.2) |> sum()[1] 7.79264e-05Gabarite a prova
A probabilidade de acerto de 10 questões é dada pela probabilidade pontual de exatamente 10 sucessos em 10 tentativas.
dbinom(x = 10, size = 10, prob = 0.2)[1] 1.024e-07Mostrar código
prova <-
tibble(nques = 0:10,
prob = dbinom(x = 0:10, size = 10, prob = 0.2),
prob_ac = cumsum(prob))
ggplot(prova, aes(nques, prob, label = round(prob, 4)))+
geom_bar(stat = "identity",
col = "black",
fill = "cyan")+
scale_x_continuous(breaks = c(0:10))+
labs(x = "Número de questões",
y = "Probabilidade")+
ggtitle(label = "Probabilidade de acerto em uma prova de 10 questões",
subtitle = "Cada questão tem 5 alternativas, apenas 1 é correta")+
scale_y_continuous(expand = expansion(mult = c(0, 0.1)))+
geom_text(vjust = -1) +
theme_grey(base_size = 14) +
theme(panel.grid.minor = element_blank())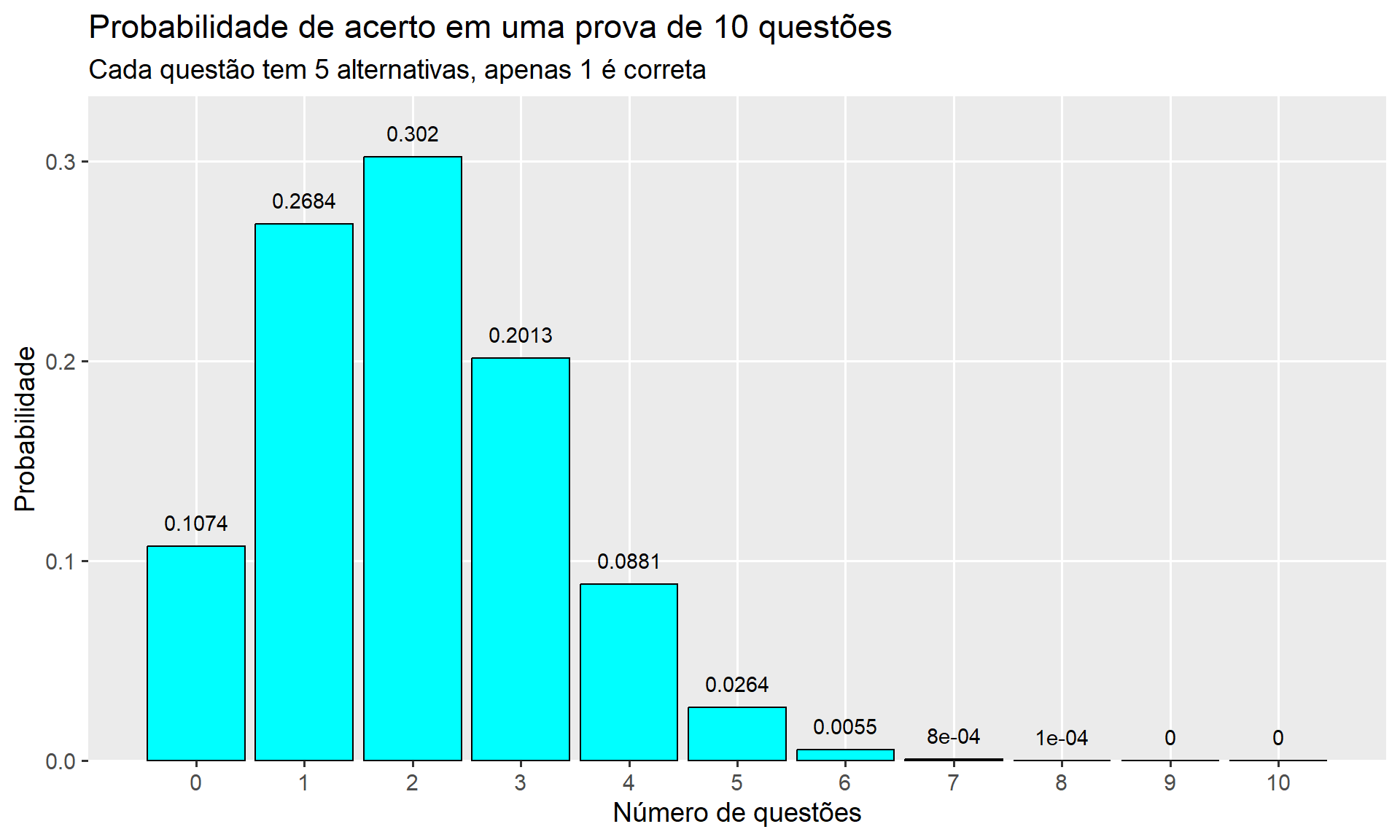
Mostrar código
# distribuição acumulada
ggplot(prova, aes(nques, prob_ac))+
geom_path(color = "red", size = 1)+
labs(x = "Número de questões",
y = "Probabilidade acumulada")+
ggtitle(label = "Probabilidade acumulada de acertar 10 questões 'chutando' todas",
subtitle = "Cada questão tem 5 alternativas, apenas 1 é correta")+
scale_x_continuous(breaks = c(0:10)) +
theme_grey(base_size = 14) +
theme(panel.grid.minor = element_blank())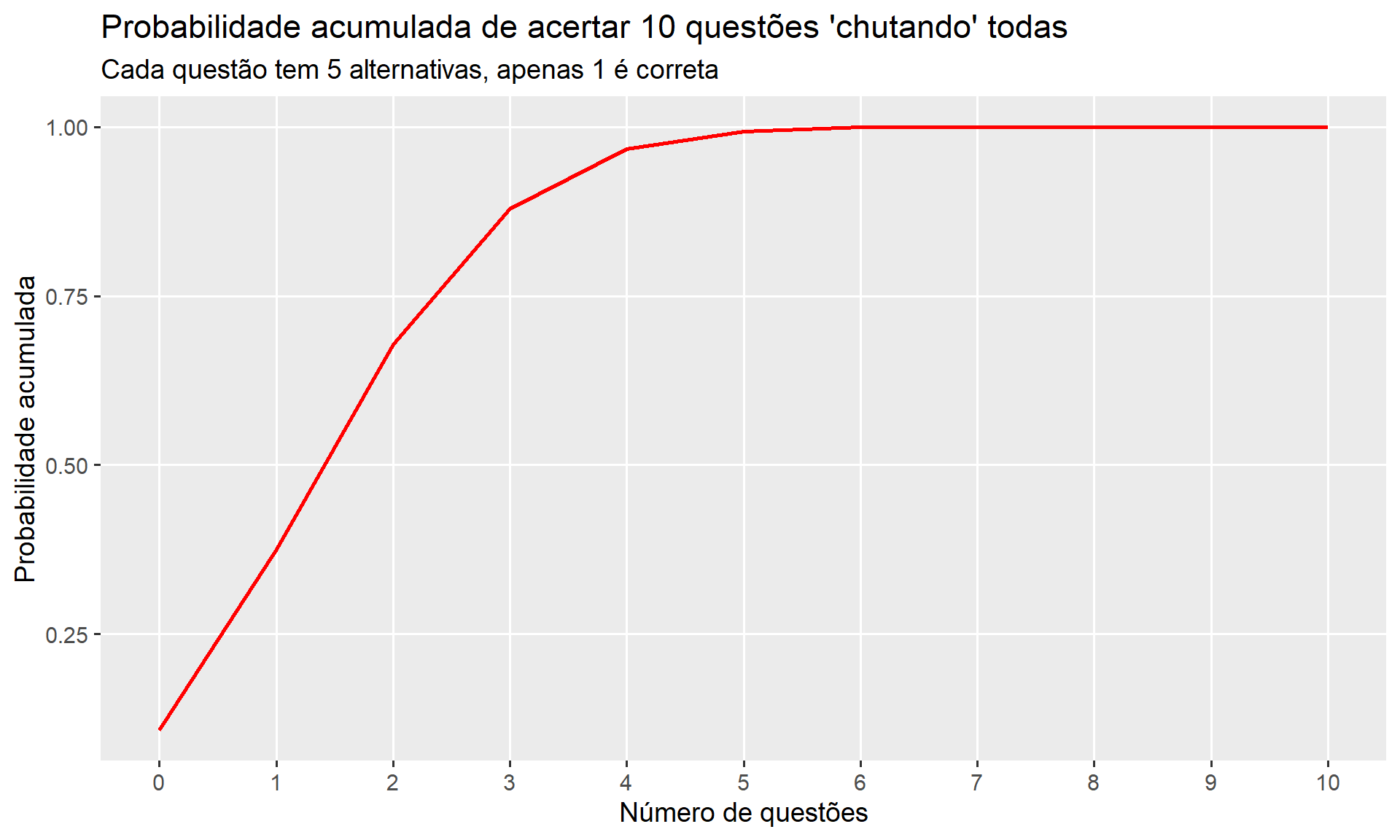
Exercício germinação de sementes
Uma empresa produtora de sementes de moranga vende pacotes com 20 sementes cada. O percentual de germinação destas sementes é de 92%. A empresa garante que pacotes que contém menos de 18 sementes germinadas são indenizados na metade do valor de venda. Se você comprou um pacote de sementes desta empresa a probabilidade de ser indenizado é de:
dbinom(0:17, size = 20, prob = 0.92) |> sum()[1] 0.2120538Exercício nascimento de bezerros
A inseminação artificial (IA) é uma das biotecnias da reprodução bovina mais importante e utilizada visando o melhoramento genético do rebanho. O uso de sêmem sexado é uma tecnologia em que os espermatozoides que vão resultar na escolha do sexo que o criador deseja, são separados daqueles que resultariam em machos após a fecundação do óvulo. Ou seja, ao final do processo obtêm-se uma paleta de sêmen com predominância de espermatozoides “fêmeas” ou “Machos”, dependendo da escolha. Portanto, a sexagem de espermatozoides permite maximizar a produção animal, possibilitando maior progresso genético entre as gerações1.
Considere um lote de 120 vacas inseminadas com sêmem sexado que contenha a probabilidade de 85% de nascimento de fêmeas. Assumindo um nascimento por fêmea, calcule a probabilidade de:
Todos os bezerros nascidos sejam fêmeas
Neste caso, a probabilidade é dada pela probabilidade pontual de 120 nascimentos de fêmeas.
dbinom(x = 120, size = 120, prob = 0.85)[1] 3.390557e-09Pelo menos 90% dos bezerros nascidos sejam fêmeas
Neste caso, precisaríamos de, pelo menos, 108 (120 \(\times\) 0,9) bezerros fêmeas. Então, a probabilidade dessa ocorrência é \(P(X \>= 108) + P(X = 109) + ... + P(X = 120)\)
x <-
data.frame(nascimentos = 108:120) |>
mutate(prob = dbinom(nascimentos, size = 120, prob = 0.85),
acum = cumsum(prob))
x nascimentos prob acum
1 108 3.260600e-02 0.03260600
2 109 2.034136e-02 0.05294736
3 110 1.152677e-02 0.06447412
4 111 5.884537e-03 0.07035866
5 112 2.679566e-03 0.07303823
6 113 1.074988e-03 0.07411322
7 114 3.740456e-04 0.07448726
8 115 1.105874e-04 0.07459785
9 116 2.701129e-05 0.07462486
10 117 5.232956e-06 0.07463009
11 118 7.539004e-07 0.07463085
12 119 7.180004e-08 0.07463092
13 120 3.390557e-09 0.07463092Multa por ineficiência
O vendedor do sêmen se comprometeu em pagar uma multa de R$10,00 para cada bezerro macho nascido se a taxa de parição de fêmeas fosse menor que 75%. Qual a probabilidade do produtor receber alguma indenização?
O produtor somente será indenizado se nascerem 89 ou menos bezerras. Assim, a probabilidade é dada pela soma das probabilidades individuais de 0 até 89
dbinom(x = 0:89, size = 120, prob = 0.85) |> sum()[1] 0.001409492# ou pbinom() que retorna a fdp acumulada
pbinom(q = 89, size = 120, prob = 0.85)[1] 0.001409492Abaixo, é possível identificar a distribuição de probabilidade para o exemplo dado.
Mostrar código
bezerros <-
tibble(nbez = 0:120,
prob = dbinom(x = 0:120, size = 120, prob = 0.85),
prob_ac = cumsum(prob))
# Gráfico da distribuição
ggplot(bezerros, aes(nbez, prob))+
geom_bar(stat = "identity",
col = "black",
size = 0.05,
fill = "cyan")+
labs(x = "Número de bezerros fêmeas",
y = "Probabilidade") +
ggtitle(label = "Probabilidade de nascimento de terneiras em 120 partos",
subtitle = "Sêmen com 85% de probabilidade de nascimento de terneiras")+
scale_y_continuous(expand = expansion(mult = c(0, 0.1)))+
scale_x_continuous(breaks = seq(0, 120, 20))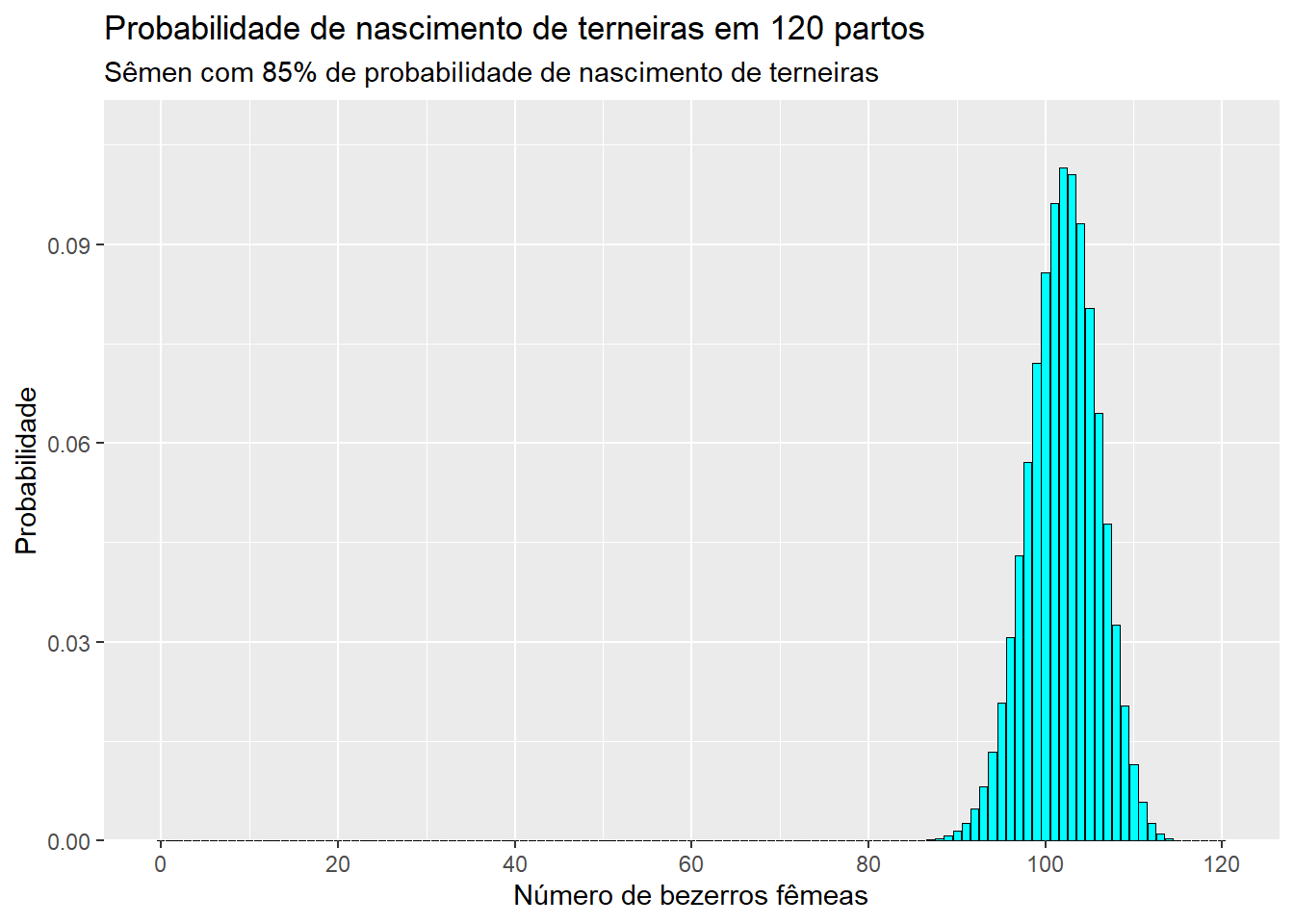
Mostrar código
# distribuição acumulada
ggplot(bezerros, aes(nbez, prob_ac))+
geom_path(color = "red", size = 1)+
labs(x = "Número de fêmeas",
y = "Probabilidade acumulada")+
ggtitle(label = "Probabilidade acumulada de nascimento de fêmeas",
subtitle = "Sêmem sexado com 85% de chance de nascimento de fêmeas")+
# scale_x_continuous(breaks = c(0:10)) +
theme_grey(base_size = 14) +
theme(panel.grid.minor = element_blank())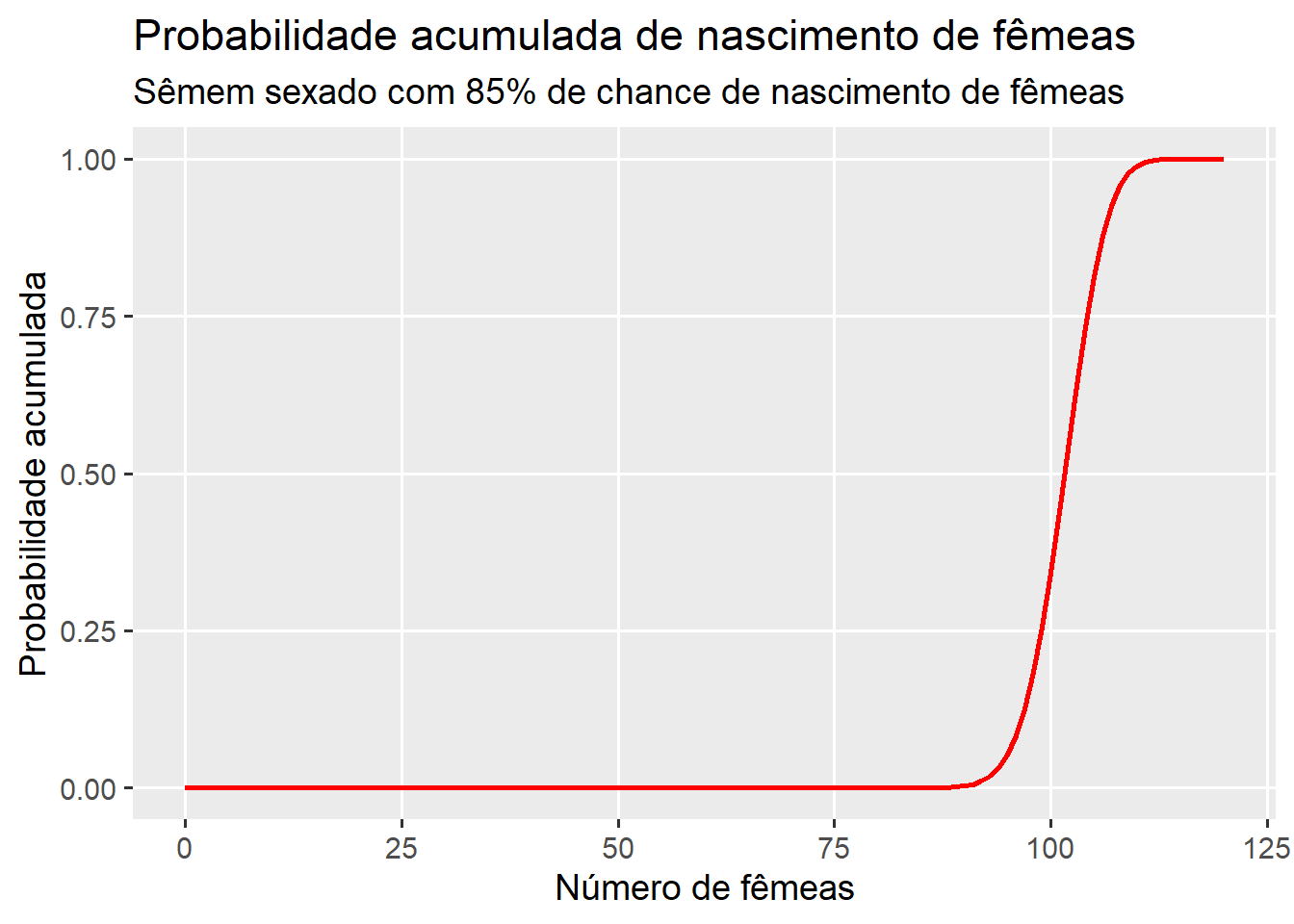
Tutorial R
Footnotes
https://cooperativa.coop.br/semen-sexado-entenda-o-que-e/↩︎