“Muito melhor uma resposta aproximada à pergunta certa, que muitas vezes é vaga, do que uma resposta exata à pergunta errada, que sempre pode ser feita com precisão.” — John Tukey
Introdução
As análises realizadas até agora tinham como objetivo verificar a existência de diferenças entre as médias de duas amostras. Porém, quando deseja-se estudar o efeito de “grupos de fatores” sobre determinado fenômeno, a análise da variância (ANOVA) é indicada. A ANOVA atribui a diversos fatores partes da variabilidade dos dados. Ela pode ser visualizada como uma técnica para examinar uma relação de dependência onde a variável de resposta (dependência) é quantitativa contínua e os fatores (variáveis independentes) são de natureza categórica com um número de categorias maior que dois.
Fisher e Mackenzie (1923) estudando a variação de diferentes cultivares de batata, publicaram o primeiro trabalho demonstrando o uso da ANOVA para a avaliação de experimentos agrícolas. O método da ANOVA se tornaria popular e amplamente utilizado após Fisher estabelecer as bases teóricas e os pressupostos desta técnica (Fisher 1925, 1935).
Os delineamentos experimentais são partes importantes da ANOVA. Em seções próprias, serão apresentados os mais comuns: o delineamento inteiramente casualisado (DIC) e o blocos ao acaso (DBC). Na seção Experimentos fatoriais são discutidos formas de arranjar os tratamentos na área experimental, como por exemplo, em parcelas subdivididas.
Princípios básicos
Os principios básicos da experimentação são a casualisação e a repetição. A repetição possibilita que o erro seja estimado; a casualisação que eles sejam independentes. Um terceiro princípio (não obrigatório) é o controle local (ou bloqueamento). O bloqueamento é utilizado no no DBC como objetivo isolar parte da variação residual do modelo DIC para uma fonte de variação conhecida (BLOCO). Com isso (principalmente quando há efeito de bloco), a precisão da análise é maior.
Repetição
Quando um tratamento é repetido, é possível estimar sua média e sua variância. Na ANOVA, então, o objetivo é testar se a variância entre os tratamentos é maior que a variância dentro dos tratamentos. No exemplo abaixo, dois cenários com médias semelhantes mas variâncias bem distintas são simulados. No primeiro, uma variância alta é utilizada.
No segundo exemplo, os dados simulados apresentam uma variação entre repetições do mesmo grupo substancialmente menor que o primeiro. Veja o que acontece.
Para realizar a casualização em um experimento de delineamento inteiramente ao acaso, pode-se utilizar a função CRD do pacote FielDHub. Neste exemplo, simulo a casualização de quatro tratamentos (“C1”, “C2”, “C3” e “C4”) em um ensaio conduzido em delineamento inteiramente casualizado (DIC) com quatro repetições (r).
Randomized Complete Block Design (RCBD):
Information on the design parameters:
List of 7
$ blocks : num 4
$ number.of.treatments: int 4
$ treatments : chr [1:4] "C1" "C2" "C3" "C4"
$ locations : num 1
$ plotNumber : num [1:4] 101 201 301 401
$ locationNames : chr "loc1"
$ seed : num 18285
10 First observations of the data frame with the RCBD field book:
ID LOCATION PLOT REP TREATMENT
1 1 loc1 101 1 C1
2 2 loc1 102 1 C4
3 3 loc1 103 1 C3
4 4 loc1 104 1 C2
8 5 loc1 201 2 C3
7 6 loc1 202 2 C2
6 7 loc1 203 2 C1
5 8 loc1 204 2 C4
9 9 loc1 301 3 C1
10 10 loc1 302 3 C4
plot(rcbd)
Exemplo de aplicação
Na figura abaixo é mostrado como o DBC pode ser utilizado para considerar fontes de variação conhecida na área experimental. Neste caso, um gradiente de fósforo conhecido é notado no solo, onde maiores valores são observados na parte inferior e menores na parte inferior. Assim, os blocos podem ser alocados de modo que cada tratamento seja casualizado dentro de grupos de unidades experimentais homogêneas (blocos).
Exemplo de casualização em DBC
Pressupostos
Independente do delineamento, os pressupostos do modelo estatístico são que os erros são independentes, homocedásticos e normais:
Esses pressupostos são necessários para que o teste F seja utilizado na análise de variância. Sob normalidade dos resíduos e hipótese nula \(H_0\), a razão entre as somas de quadrado de tratamento e resíduo tem distribuição F (Rencher and Schaalje 2008). Já em condições de não normalidade dos resíduos, o poder do teste (probabilidade de rejeitar \(H_0\)) é reduzido. Apesar disso, não há grandes mudanças no erro tipo I quando a pressuposição de normalidade é violada (Senoglu and Tiku 2001), e por isso ele é considerado robusto.
Abaixo, é apresentada a distribuição F considerando 4 e 20 como graus liberdade do tratamento e erro, respectivamente. Note que o valor em x em que acumula à direita 0,05 é o conhecido F tabelado.
Os dados utilizados neste exemplo estão na planilha QUALI do conjunto de dados data_R.xlsx. Os próximos códigos carregam o conjunto de dados e criam um gráfico do tipo boxplot para explorar o padrão dos dados.
Analizando o boxplot acima é razoável dizer que as médias dos tratamentos são diferentes, principalmente comparando o NP_1 com NP_5. Esta suspeita de diferença, no entanto, deve ser suportada com a realização da análise de variância.
Anova em DIC
No pacote AgroR, quando os fatores são qualitativos, a análise complementar aplicada é a comparção de médias. A função DIC() do pacote retorna a tabela da ANOVA, a análise de pressupostos (normalidade e homogeneidade) e o teste de comparação de médias.
mod_dic <-with(df, DIC(HIBRIDO, RG))
-----------------------------------------------------------------
Normality of errors
-----------------------------------------------------------------
Method Statistic p.value
Shapiro-Wilk normality test(W) 0.827455 0.002285375
-----------------------------------------------------------------
Homogeneity of Variances
-----------------------------------------------------------------
Method Statistic p.value
Bartlett test(Bartlett's K-squared) 0.9557917 0.9164237
-----------------------------------------------------------------
Independence from errors
-----------------------------------------------------------------
Method Statistic p.value
Durbin-Watson test(DW) 0.3899192 3.318679e-05
-----------------------------------------------------------------
Additional Information
-----------------------------------------------------------------
CV (%) = 23.06
MStrat/MST = 0.69
Mean = 8.2479
Median = 8.0515
Possible outliers = No discrepant point
-----------------------------------------------------------------
Analysis of Variance
-----------------------------------------------------------------
Df Sum Sq Mean.Sq F value Pr(F)
Treatment 4 32.62995 8.157488 2.254327 0.1117755
Residuals 15 54.27888 3.618592
-----------------------------------------------------------------
Multiple Comparison Test: Tukey HSD
-----------------------------------------------------------------
[1] "H0 is not rejected"
Tip
As funções do pacote AgroR utilizam os dados “anexados” ao ambiente de trabalho, ou seja, um argumento data = . não existe para suas funções. Note que no exemplo acima foi utilizado a função with(qualitativo, DIC(...)). Isto permite acessar variáveis presentes no data frame. Uma outra maneira de realizar esta mesma análise é utilizando a função attach(df), qual carregará o data frame no ambiente R, assim é possível utilizar a função DIC(...). Após realizada a análise, é recomendado executar o comando detach(df) para “limpar” os dados do ambiente de trabalho.
A interpretação da significância, ou seja, se as médias de produtividade dos híbridos foram significativamente diferentes a uma determinada probabilidade de erro é feita verificando-se o valor de "Pr>fc" na ANOVA. A figura abaixo mostra a distribuição F considerando os graus de liberdade de tratamento e erro \(F_{4, 15}\) e nos ajuda a compreender um pouco melhor isto.
O valor de F calculado em nosso exemplo foi de 2,2543, o que resulta em uma probabilidade de erro acumulada de 0,1117 (11,17%). Esta probabilidade de erro acumulada está representada pela cor vermelha. Logo, não rejeitou-se a hipótese Para que uma diferença significativa a 5% de probabilidade de erro tivesse sido observada, o valor de F calculado deveria ter sido 3,055 qf(0.05, 4, 15, lower.tail = FALSE), representado neste caso pela cor verde no gráfico.
Considerando nosso exemplo, parece razoável dizer que 9,48 t (NP_1) é uma produção maior que 6,28 t (NP_5). Então, é justo perguntar: O que pode ter acontecido para que as médias não tenham sido consideradas diferentes considerando a probabilidade de erro, mesmo tendo fortes indícios de que elas seriam? A primeira opção que nos vem a mente –e que na maioria das vezes é encontrada em artigos científicos– é que as alterações no rendimento de grão observadas fora resultado do acaso; ou seja, neste caso, há a probabilidade de 11,17% de que uma diferença pelo menos tão grande quanto a observada no estudo possa ser gerada a partir de amostras aleatórias se os tratamentos não aferatem a variável resposta. Logo, a recomendação estatística neste caso, seria por optar por qualquer um dos tratamentos. Do ponto de vista prático, sabemos que esta recomendação está totalmente equivocada. Neste ponto surge uma importante (e polêmica) questão: a interpretação do p-valor. Um p-valor de 0,05 não significa que há uma chance de 95% de que determinada hipótese esteja correta. Em vez disso, significa que se a hipótese nula for verdadeira e todas as outras suposições feitas forem válidas, haverá 5% de chance que diferenças ao menos tão grandes quanto as observadas podem ser obtidas de amostras aleatórias. É preciso ter em mente que o p-valor relatado pelos testes é um significado probabilístico, não biológico. Assim, em experimentos biológicos, a interpretação desta estatística deve ser cautelosa, pois um p-valor pode não indicar a importância de uma descoberta. Por exemplo, um medicamento pode ter um efeito estatisticamente significativo nos níveis de glicose no sangue dos pacientes sem ter um efeito terapêutico. Sugerimos a leitura de cinco interessantes artigos relacionados a este assunto (Altman and Krzywinski 2017; Baker 2016; Singh Chawla 2017; Krzywinski and Altman 2013; Nuzzo 2014).
Em adição à justificativa anterior (as alterações no rendimento de grão observadas fora resultado do acaso), existem pelo menos mais três razões potenciais para a não regeição da hipótese \(H_0\) em nosso exemplo:
um experimento mal projetado com poder insuficiente para detectar uma diferença (à 5% de erro) entre as médias;
os tratamentos foram mal escolhidos e não refletiram adequadamente a hipótese inicial do estudo
o experimento foi indevidamente instalado e conduzido sem supervisão adequada, com baixo controle de qualidade sobre os protocolos de tratamento, coleta e análise de dados.
Esta última opção parece ser a mais razoável aqui. É possivel observar no boxplot para o fator bloco que o bloco 4 parece ter uma média superior aos outros blocos. Sabe-ser que no DIC, toda diferença entre as repetições de um mesmo tratamento comporão o erro experimental. Logo, neste exemplo, a área experimental não era homogênea como se pressupunha na instalação do experimento. Isto ficará claro, posteriormente, ao analisarmos o mesmo conjunto de dados, no entanto considerando um DBC.
As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, the variances can be considered homogeneous
As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered independent
-----------------------------------------------------------------
Additional Information
-----------------------------------------------------------------
CV (%) = 8.2
MStrat/MST = 0.33
Mean = 8.2479
Median = 8.0515
Possible outliers = No discrepant point
-----------------------------------------------------------------
Analysis of Variance
-----------------------------------------------------------------
Df Sum Sq Mean.Sq F value Pr(F)
Treatment 4 32.629952 8.1574881 17.8475 5.449170e-05
Block 3 48.794088 16.2646961 35.5850 2.983658e-06
Residuals 12 5.484793 0.4570661
As the calculated p-value, it is less than the 5% significance level. The hypothesis H0 of equality of means is rejected. Therefore, at least two treatments differ
-----------------------------------------------------------------
Multiple Comparison Test: Tukey HSD
-----------------------------------------------------------------
resp groups
NP_2 9.48075 a
NP_1 9.48000 a
NP_3 8.75075 ab
NP_4 7.24500 bc
NP_5 6.28300 c
Fisher, R. A. 1925. Statistical Methods for Research Workers. Edinburgh: Oliver; Boyd.
———. 1935. The Design of Experiments. Edinburgh: Oliver; Boyd.
Fisher, R. A., and W. A. Mackenzie. 1923. “Studies in Crop Variation. II. The Manurial Response of Different Potato Varieties.”The Journal of Agricultural Science 13 (3): 311–20. https://doi.org/10.1017/s0021859600003592.
Krzywinski, Martin, and Naomi Altman. 2013. “Significance, P Values and t-Tests.”Nature Methods 10 (11): 1041–42. https://doi.org/10.1038/nmeth.2698.
Rencher, Alvin C., and G. Bruce. Schaalje. 2008. Linear Models in Statistics. John Wiley & Sons.
Senoglu, Birdal, and Moti L. Tiku. 2001. “Analysis of Variance in Experimental Design with Nonnormal Error Distributions.”Communications in Statistics - Theory and Methods 30 (7): 1335–52. https://doi.org/10.1081/STA-100104748.
---title: "7. Análise de Variância"bibliography: references.bibexecute: out-width: maxwidth---::: callout-tip"Muito melhor uma resposta aproximada à pergunta certa, que muitas vezes é vaga, do que uma resposta exata à pergunta errada, que sempre pode ser feita com precisão." --- John Tukey:::# IntroduçãoAs análises realizadas até agora tinham como objetivo verificar a existência de diferenças entre as médias de duas amostras. Porém, quando deseja-se estudar o efeito de "grupos de fatores" sobre determinado fenômeno, a análise da variância (ANOVA) é indicada. A ANOVA atribui a diversos fatores partes da variabilidade dos dados. Ela pode ser visualizada como uma técnica para examinar uma relação de dependência onde a variável de resposta (dependência) é quantitativa contínua e os fatores (variáveis independentes) são de natureza categórica com um número de categorias maior que dois.Fisher e Mackenzie [-@fisher1923a] estudando a variação de diferentes cultivares de batata, publicaram o primeiro trabalho demonstrando o uso da ANOVA para a avaliação de experimentos agrícolas. O método da ANOVA se tornaria popular e amplamente utilizado após Fisher estabelecer as bases teóricas e os pressupostos desta técnica [@Fisher1925; @Fisher1935].Os delineamentos experimentais são partes importantes da ANOVA. Em seções próprias, serão apresentados os mais comuns: o delineamento inteiramente casualisado (DIC) e o blocos ao acaso (DBC). Na seção [Experimentos fatoriais](https://tiagoolivoto.github.io/classes/FIT5306/FIT5306_10_FAT.html) são discutidos formas de arranjar os tratamentos na área experimental, como por exemplo, em parcelas subdivididas.# Princípios básicosOs principios básicos da experimentação são a **casualisação** e a **repetição**. A repetição possibilita que o erro seja estimado; a casualisação que eles sejam independentes. Um terceiro princípio (não obrigatório) é o **controle local** (ou bloqueamento). O bloqueamento é utilizado no no DBC como objetivo isolar parte da variação residual do modelo DIC para uma fonte de variação conhecida (BLOCO). Com isso (principalmente quando há efeito de bloco), a precisão da análise é maior.# RepetiçãoQuando um tratamento é repetido, é possível estimar sua média e sua variância. Na ANOVA, então, o objetivo é testar se a variância entre os tratamentos é maior que a variância dentro dos tratamentos. No exemplo abaixo, dois cenários com médias semelhantes mas variâncias bem distintas são simulados. No primeiro, uma variância alta é utilizada.```{r}#| code-fold: true#| out-width: "100%"#| message: false#| warning: false#| fig-height: 2library(tidyverse)parms <-data.frame(name =c("g1", "g2", "g3"),mu =c(10, 13, 18),sd =c(1.5, 1.2, 1.8))ggplot() +stat_function(fun=dnorm,geom="line",aes(color ="g1"),size =1.5,n =1000,args =list(mean = parms$mu[1], sd = parms$sd[1])) +stat_function(fun=dnorm,geom="line",aes(color ="g2"),size =1.5,n =1000,args =list(mean = parms$mu[2], sd = parms$sd[2])) +stat_function(fun=dnorm,geom="line",aes(color ="g3"),size =1.5,n =1000,args =list(mean = parms$mu[3], sd = parms$sd[3])) +geom_vline(aes(xintercept = mu, color = name), data = parms,size =1.5) +geom_vline(xintercept =mean(parms$mu)) +scale_color_manual(values = metan::ggplot_color(4)) +scale_y_continuous(breaks =NULL,expand =expansion(c(0, 0.1))) +xlim(c(5, 25)) +theme_bw() +theme(panel.grid =element_blank())```No segundo exemplo, os dados simulados apresentam uma variação entre repetições do mesmo grupo substancialmente menor que o primeiro. Veja o que acontece.```{r}#| code-fold: true#| out-width: "100%"#| message: false#| warning: false#| fig-height: 2# low varianceparms <-data.frame(name =c("g1", "g2", "g3"),mu =c(10, 13, 18),sd =c(0.6, 0.7, 0.6))ggplot() +stat_function(fun=dnorm,geom="line",aes(color ="g1"),size =1.5,n =1000,args =list(mean = parms$mu[1], sd = parms$sd[1])) +stat_function(fun=dnorm,geom="line",aes(color ="g2"),size =1.5,n =1000,args =list(mean = parms$mu[2], sd = parms$sd[2])) +stat_function(fun=dnorm,geom="line",aes(color ="g3"),size =1.5,n =1000,args =list(mean = parms$mu[3], sd = parms$sd[3])) +geom_vline(aes(xintercept = mu, color = name), data = parms,size =1.5) +geom_vline(xintercept =mean(parms$mu)) +scale_color_manual(values = metan::ggplot_color(4)) +scale_y_continuous(breaks =NULL,expand =expansion(c(0, 0.1))) +xlim(c(5, 25)) +theme_bw() +theme(panel.grid =element_blank())```# Casualização## DICPara realizar a casualização em um experimento de delineamento inteiramente ao acaso, pode-se utilizar a função `CRD` do pacote FielDHub. Neste exemplo, simulo a casualização de quatro tratamentos ("C1", "C2", "C3" e "C4") em um ensaio conduzido em delineamento inteiramente casualizado (DIC) com quatro repetições (`r`).```{r}#| out-width: "100%"#| library(FielDHub)trats <-c("C1", "C2", "C3", "C4")crd <-CRD(t = trats,reps =4)print(crd)plot(crd)```## DBCPara casualização em DBC, `RCBD` é usada.```{r}#| out-width: "100%"trats <-c("C1", "C2", "C3", "C4")rcbd <-RCBD(t = trats,reps =4)print(rcbd)plot(rcbd)```## Exemplo de aplicaçãoNa figura abaixo é mostrado como o DBC pode ser utilizado para considerar fontes de variação conhecida na área experimental. Neste caso, um gradiente de fósforo conhecido é notado no solo, onde maiores valores são observados na parte inferior e menores na parte inferior. Assim, os blocos podem ser alocados de modo que cada tratamento seja casualizado dentro de grupos de unidades experimentais homogêneas (blocos).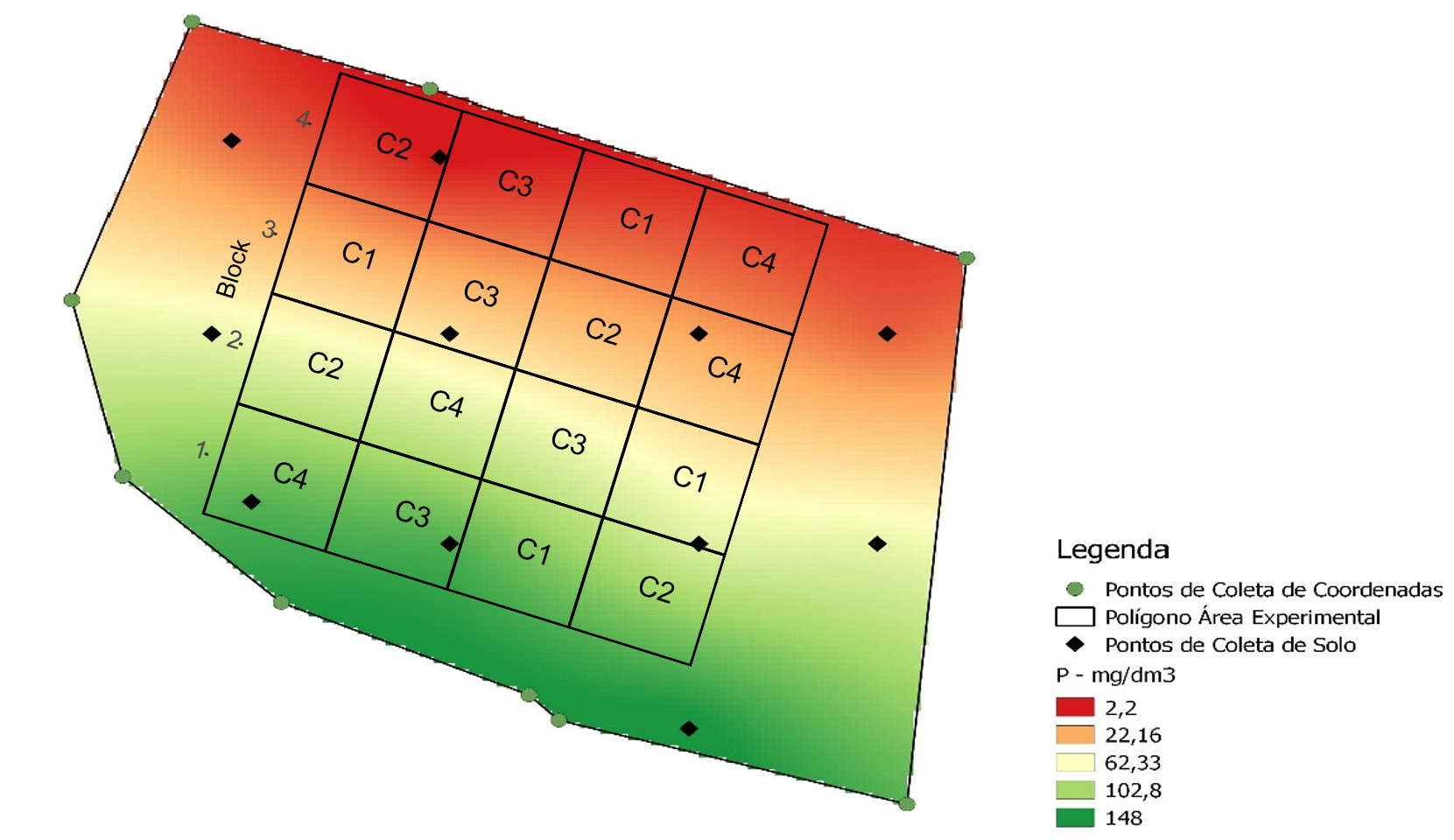# PressupostosIndependente do delineamento, os pressupostos do modelo estatístico são que os erros são independentes, homocedásticos e normais:$${\boldsymbol{\varepsilon }} \sim {\textrm N}\left( {0,{\boldsymbol{I}}{\sigma ^2}} \right)$$# Distribuição FEsses pressupostos são necessários para que o teste F seja utilizado na análise de variância. Sob normalidade dos resíduos e hipótese nula $H_0$, a razão entre as somas de quadrado de tratamento e resíduo tem distribuição F [@Rencher2008]. Já em condições de não normalidade dos resíduos, o poder do teste (probabilidade de rejeitar $H_0$) é reduzido. Apesar disso, não há grandes mudanças no erro tipo I quando a pressuposição de normalidade é violada [@senoglu2001], e por isso ele é considerado robusto.Abaixo, é apresentada a distribuição F considerando 4 e 20 como graus liberdade do tratamento e erro, respectivamente. Note que o valor em x em que acumula à direita 0,05 é o conhecido F tabelado.```{r}#| out-width: "100%"#| code-fold: true#| code-summary: "Mostrar código"library(ggplot2)df1 <-4df2 <-20(ftab <-qf(0.05, df1, df2, lower.tail =FALSE))ggplot() +scale_x_continuous(limits =c(0, 6),breaks =c(0, 2, ftab, 4, 6)) +stat_function(fun = df,geom ="area",fill ="forestgreen",xlim =c(ftab, 6),args =list(df1 = df1,df2 = df2 )) +stat_function(fun = df,geom ="line",size =1,args =list(df1 = df1,df2 = df2 )) +theme_bw(base_size =16) +theme(panel.grid.minor =element_blank()) +scale_y_continuous(expand =expansion(mult =c(0, .1)))+labs(x ="Valor de F",y ="Probabilidade acumulada",title ="Distribuição F (DF1: 4, DF2: 20)")```# Um exemplo## DadosOs dados utilizados neste exemplo estão na planilha `QUALI` do conjunto de dados `data_R.xlsx`. Os próximos códigos carregam o conjunto de dados e criam um gráfico do tipo boxplot para explorar o padrão dos dados.```{r echo = TRUE, eval = TRUE, message = FALSE, warning = FALSE}#| out-width: "100%"#| fig-width: 12#| fig-height: 4library(tidyverse)library(metan)library(rio)library(AgroR)url <-"http://bit.ly/df_biostat"df <-import(url, sheet ="QUALI")str(df)p1 <-ggplot(df, aes(HIBRIDO, RG))+geom_hline(yintercept =mean(df$RG), linetype ="dashed")+geom_boxplot()+stat_summary(geom ="point", fun = mean, shape =23) +stat_summary(aes(label =round(after_stat(y), 2),x = HIBRIDO), fun=mean,geom="text",hjust=-0.3)p2 <-ggplot(df, aes(factor(BLOCO), RG))+geom_hline(yintercept =mean(df$RG), linetype ="dashed")+geom_boxplot()+stat_summary(geom ="point", fun = mean, shape =23) +stat_summary(aes(label =round(after_stat(y), 2),x = BLOCO), fun=mean,geom="text",hjust=-0.3)p1 + p2```Analizando o boxplot acima é razoável dizer que as médias dos tratamentos são diferentes, principalmente comparando o `NP_1` com `NP_5`. Esta suspeita de diferença, no entanto, deve ser suportada com a realização da análise de variância.## Anova em DICNo pacote `AgroR`, quando os fatores são qualitativos, a análise complementar aplicada é a comparção de médias. A função `DIC()` do pacote retorna a tabela da ANOVA, a análise de pressupostos (normalidade e homogeneidade) e o teste de comparação de médias.```{r echo = TRUE, eval = TRUE, message = FALSE, warning = FALSE}mod_dic <-with(df, DIC(HIBRIDO, RG))```::: callout-tipAs funções do pacote **AgroR** utilizam os dados "anexados" ao ambiente de trabalho, ou seja, um argumento `data = .` não existe para suas funções. Note que no exemplo acima foi utilizado a função `with(qualitativo, DIC(...))`. Isto permite acessar variáveis presentes no data frame. Uma outra maneira de realizar esta mesma análise é utilizando a função `attach(df)`, qual carregará o data frame no ambiente R, assim é possível utilizar a função `DIC(...)`. Após realizada a análise, é recomendado executar o comando `detach(df)` para "limpar" os dados do ambiente de trabalho.:::A interpretação da significância, ou seja, se as médias de produtividade dos híbridos foram significativamente diferentes a uma determinada probabilidade de erro é feita verificando-se o valor de `"Pr>fc"` na ANOVA. A figura abaixo mostra a distribuição *F* considerando os graus de liberdade de tratamento e erro $F_{4, 15}$ e nos ajuda a compreender um pouco melhor isto.```{r eval=FALSE, results='hold'}#| code-fold: true#| code-summary: "Veja o código que gerou o gráfico"df1 <-4df2 <-15fcal <-2.2543ftab <-3.055ggplot() +scale_x_continuous(limits =c(0, 6),breaks =c(0, fcal, ftab, 6)) +stat_function(fun = df,geom ="area",fill ="red",xlim =c(fcal, 6),args =list(df1 = df1,df2 =63 )) +stat_function(fun = df,geom ="area",fill ="forestgreen",xlim =c(ftab, 6),args =list(df1 = df1,df2 =63 )) +stat_function(fun = df,geom ="line",size =1,args =list(df1 = df1,df2 =63 )) +theme_bw(base_size =16) +theme(panel.grid.minor =element_blank()) +scale_y_continuous(expand =expansion(mult =c(0, .1)))+labs(x ="Valor de F",y ="Probabilidade acumulada",title ="Distribuição F (DF1: 4, DF2: 15)")```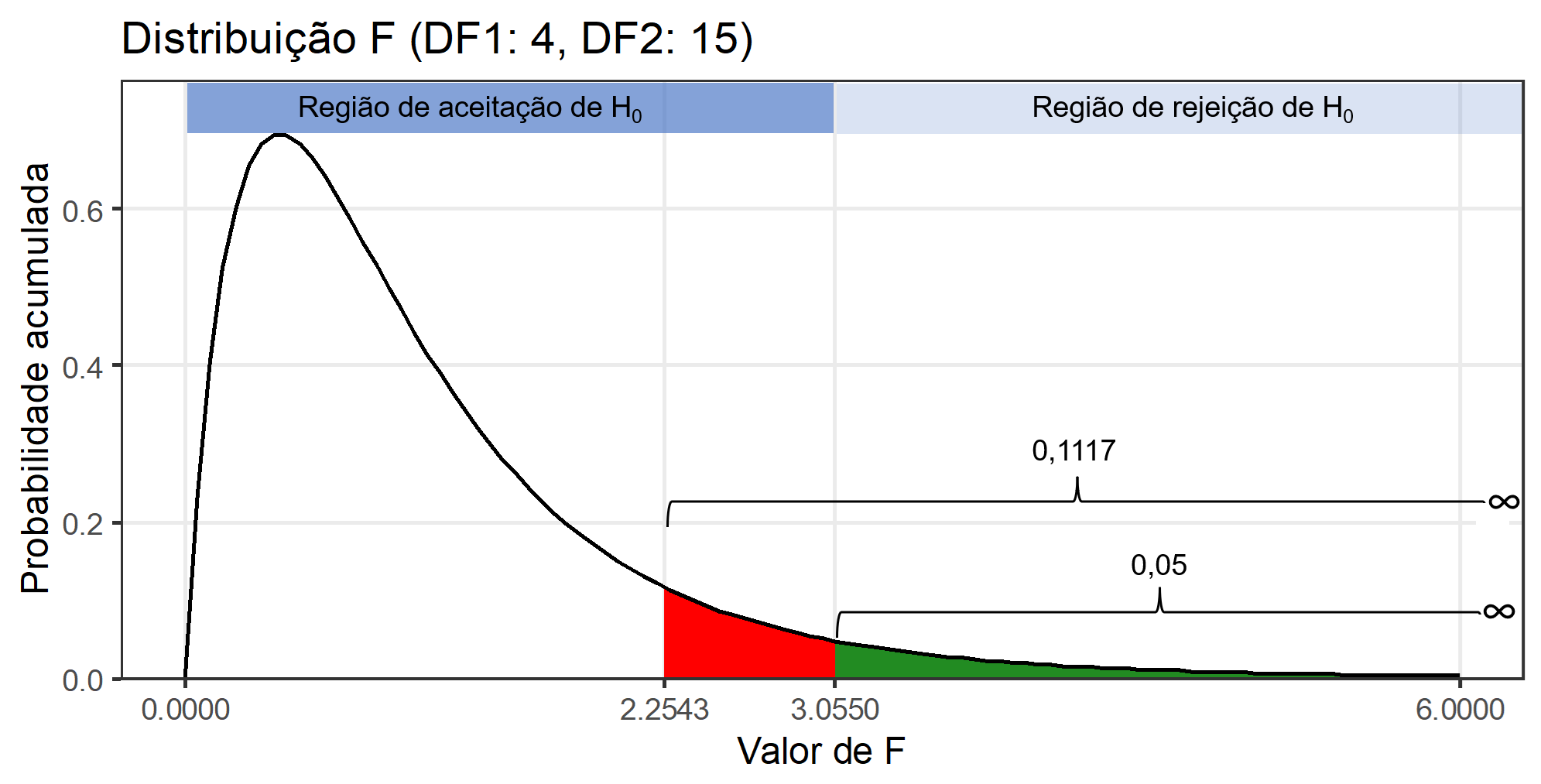{fig-align="center"}O valor de *F* calculado em nosso exemplo foi de 2,2543, o que resulta em uma probabilidade de erro acumulada de 0,1117 (11,17%). Esta probabilidade de erro acumulada está representada pela cor vermelha. Logo, não rejeitou-se a hipótese Para que uma diferença significativa a 5% de probabilidade de erro tivesse sido observada, o valor de *F* calculado deveria ter sido 3,055 `qf(0.05, 4, 15, lower.tail = FALSE)`, representado neste caso pela cor verde no gráfico.Considerando nosso exemplo, parece razoável dizer que 9,48 t (NP_1) é uma produção maior que 6,28 t (NP_5). Então, é justo perguntar: O que pode ter acontecido para que as médias não tenham sido consideradas diferentes considerando a probabilidade de erro, mesmo tendo fortes indícios de que elas seriam? A primeira opção que nos vem a mente --e que na maioria das vezes é encontrada em artigos científicos-- é que as alterações no rendimento de grão observadas fora resultado do acaso; ou seja, neste caso, há a probabilidade de 11,17% de que uma diferença pelo menos tão grande quanto a observada no estudo possa ser gerada a partir de amostras aleatórias se os tratamentos não aferatem a variável resposta. Logo, a **recomendação estatística** neste caso, seria por optar por qualquer um dos tratamentos. Do ponto de vista prático, sabemos que esta recomendação está totalmente equivocada. Neste ponto surge uma importante (e polêmica) questão: a interpretação do *p*-valor. Um *p*-valor de 0,05 não significa que há uma chance de 95% de que determinada hipótese esteja correta. Em vez disso, significa que se a hipótese nula for verdadeira e todas as outras suposições feitas forem válidas, haverá 5% de chance que diferenças ao menos tão grandes quanto as observadas podem ser obtidas de amostras aleatórias. É preciso ter em mente que o *p*-valor relatado pelos testes é um significado probabilístico, não biológico. Assim, em experimentos biológicos, a interpretação desta estatística deve ser cautelosa, pois um *p*-valor pode não indicar a importância de uma descoberta. Por exemplo, um medicamento pode ter um efeito estatisticamente significativo nos níveis de glicose no sangue dos pacientes sem ter um efeito terapêutico. Sugerimos a leitura de cinco interessantes artigos relacionados a este assunto [@altman2017; @baker2016; @singhchawla2017; @krzywinski2013; @nuzzo2014].Em adição à justificativa anterior (as alterações no rendimento de grão observadas fora resultado do acaso), existem pelo menos mais três razões potenciais para a não regeição da hipótese $H_0$ em nosso exemplo:1. um experimento mal projetado com poder insuficiente para detectar uma diferença (à 5% de erro) entre as médias;2. os tratamentos foram mal escolhidos e não refletiram adequadamente a hipótese inicial do estudo3. o experimento foi indevidamente instalado e conduzido sem supervisão adequada, com baixo controle de qualidade sobre os protocolos de tratamento, coleta e análise de dados.Esta última opção parece ser a mais razoável aqui. É possivel observar no boxplot para o fator bloco que o bloco 4 parece ter uma média superior aos outros blocos. Sabe-ser que no DIC, toda diferença entre as repetições de um mesmo tratamento comporão o erro experimental. Logo, neste exemplo, a área experimental não era homogênea como se pressupunha na instalação do experimento. Isto ficará claro, posteriormente, ao analisarmos o mesmo conjunto de dados, no entanto considerando um DBC.## Anova em DBC```{r}with(df,DBC(HIBRIDO, BLOCO, RG))``````{=html}<div align='center'><a href='https://www.free-website-hit-counter.com'><img src='https://www.free-website-hit-counter.com/c.php?d=9&id=138597&s=2' border='0' alt='Free Website Hit Counter'></a><br / ><small><a href='https://www.free-website-hit-counter.com' title="Free Website Hit Counter">Free website hit counter</a></small></div>```
