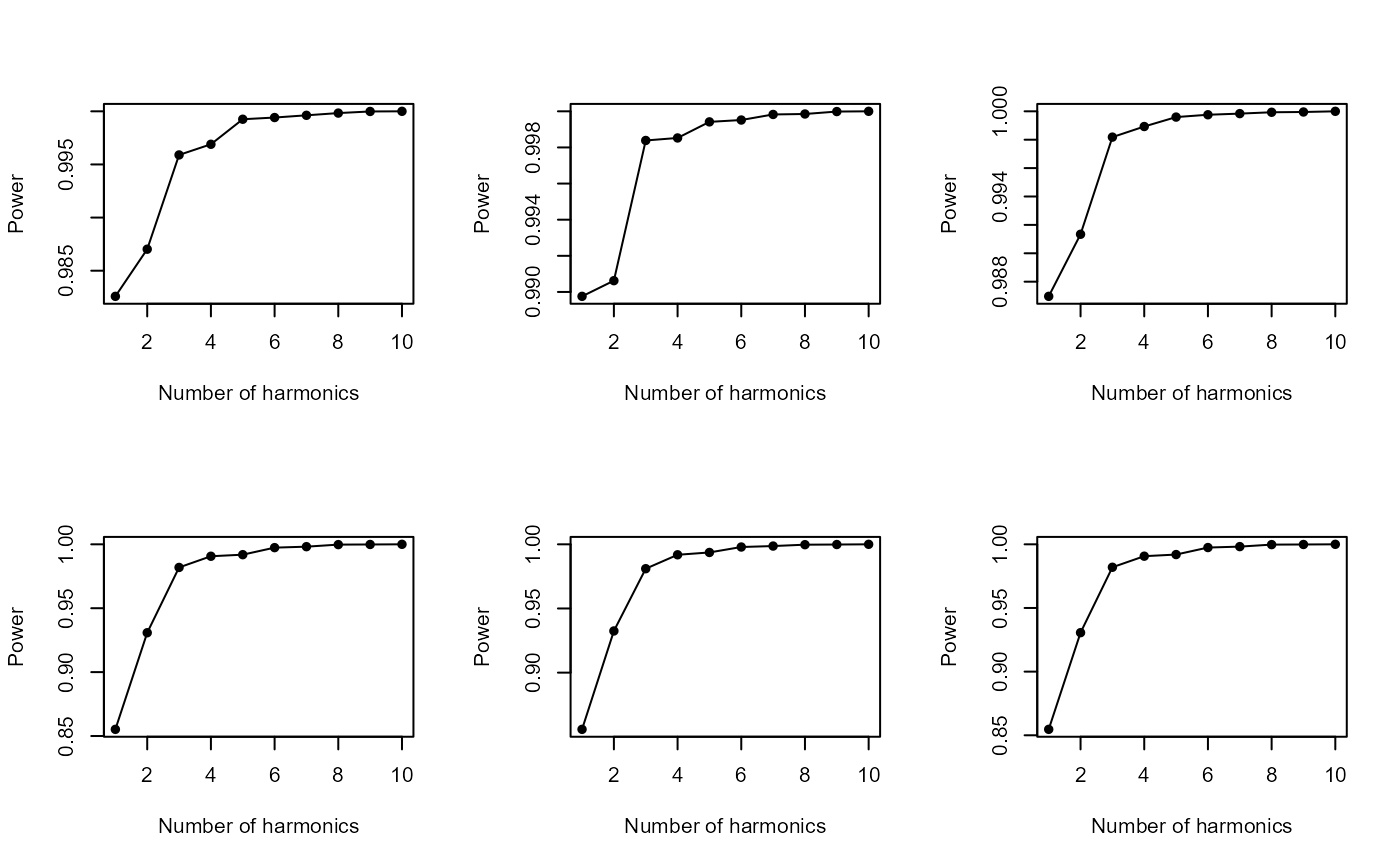
Computes an spectrum of harmonic Fourier power. The power is proportional to the harmonic amplitude and can be considered as a measure of shape information. As the rank of harmonic increases, the power decreases and adds less and less information. We can evaluate the number of harmonics that we must select, so their cumulative power gathers 99% of the total cumulative power (Claude, 2008).
Usage
efourier_power(
x,
first = TRUE,
thresh = c(0.8, 0.85, 0.9, 0.95, 0.99, 0.999),
plot = TRUE,
ncol = NULL,
nrow = NULL
)Arguments
- x
An object of class
efouriercomputed withefourier().- first
Logical argument indicating whether to include the first harmonic for computing the power. See
Details.- thresh
A numeric vector indicating the threshold power. The number of harmonics needed for such thresholds will then be computed.
- plot
Logical argument indicating whether to produce a plot.
- ncol, nrow
The number of rows or columns in the plot grid. Defaults to
NULL, i.e., a square grid is produced.
Value
A list with the objects:
cum_power, adata.frameobject with the accumulated power depending on the number of harmonics
Details
Most of the shape "information" is contained in the first harmonic.
This is not surprising because this is the harmonic that best fits the
outline, and the size of ellipses decreases as for explaining successive
residual variation. However, one may think that the first ellipse does not
contain relevant shape information, especially when differences one wants
to investigate concern complex outlines. By using first = FALSE it is
possible to remove the first harmonic for this computation. When working on
a set of outlines, high-rank-harmonics can contain information that may
allow groups to be distinguished (Claude, 2008).
Adapted from Claude (2008). pp. 229.