SL <- select(iris, Sepal.Length)Error in select(iris, Sepal.Length): não foi possível encontrar a função "select"O artigo R: A Language for Data Analysis and Graphics1, escrito pelos desenvolvedores da linguagem George Ross Ihaka e Robert Clifford Gentleman, marca o início de uma nova era no processamento e análise de dados: o desenvolvimento do software R.

O R é uma linguagem e ambiente estatístico que traz muitas vantagens para o usuário, embora elas não sejam tão obvias inicialmente:
No software R, todos os comandos são digitados e o mouse é pouco usado. Pode parecer antigo, pouco amigável ou até pobre em recursos visuais, mas isso faz com que nos deparemos com o melhor recurso do R: a sua flexibilidade. Para usuários familiarizados, a linguagem do R se torna clara e simples. Com poucos comandos, funções poderosas podem ser5 e o usuário é sempre consciente do que foi pedido através da ELC (Meus dados, minhas análises!). Isso contrasta com pacotes que possuem uma interface amigável (point-and-click), mas que escondem a dinâmica dos cálculos e, potencialmente, os seus erros. Finalmente, o R fornece uma ampla variedade de procedimentos estatísticos básicos ou que exigem grande esforço computacional (modelagem linear e não linear, testes estatísticos clássicos, análise de séries temporais, classificação, agrupamento, etc.) e recursos gráficos elegantes. Um dos pontos fortes de R é a facilidade com que gráficos de qualidade podem ser produzidos, incluindo símbolos matemáticos e fórmulas, quando necessário. O software R está disponível em uma ampla variedade de plataformas UNIX e sistemas similares (incluindo FreeBSD e Linux), Windows e MacOS.
Quem ja é usuário de softwares por linhas de comando, como o SAS, provavelmente não vai notar muita diferença. Toda análise se resume à seguinte sequência dados > códigos > saída. A experiência do usuário com o R, no entanto, pode ser mais atrativa utilizando o RStudio6. O Rstudio é um produto de código aberto disponível publicamente em 28/02/2011 que está disponível gratuitamente. Ele é um ambiente de desenvolvimento integrado para R que inclui
Nesta seção serão abordados alguns aspectos básicos para que o usuário do R possa desenvolver as suas análises. Será dado enfoque para áreas básicas da interface, cujo conhecimento é necessário para que um usuário inicante possa realizar sua primeira análisee. A figura abaixo mostra as principais janelas do Rstudio, incluindo o script, o console, a “área de trabalho” e o output para gráficos.
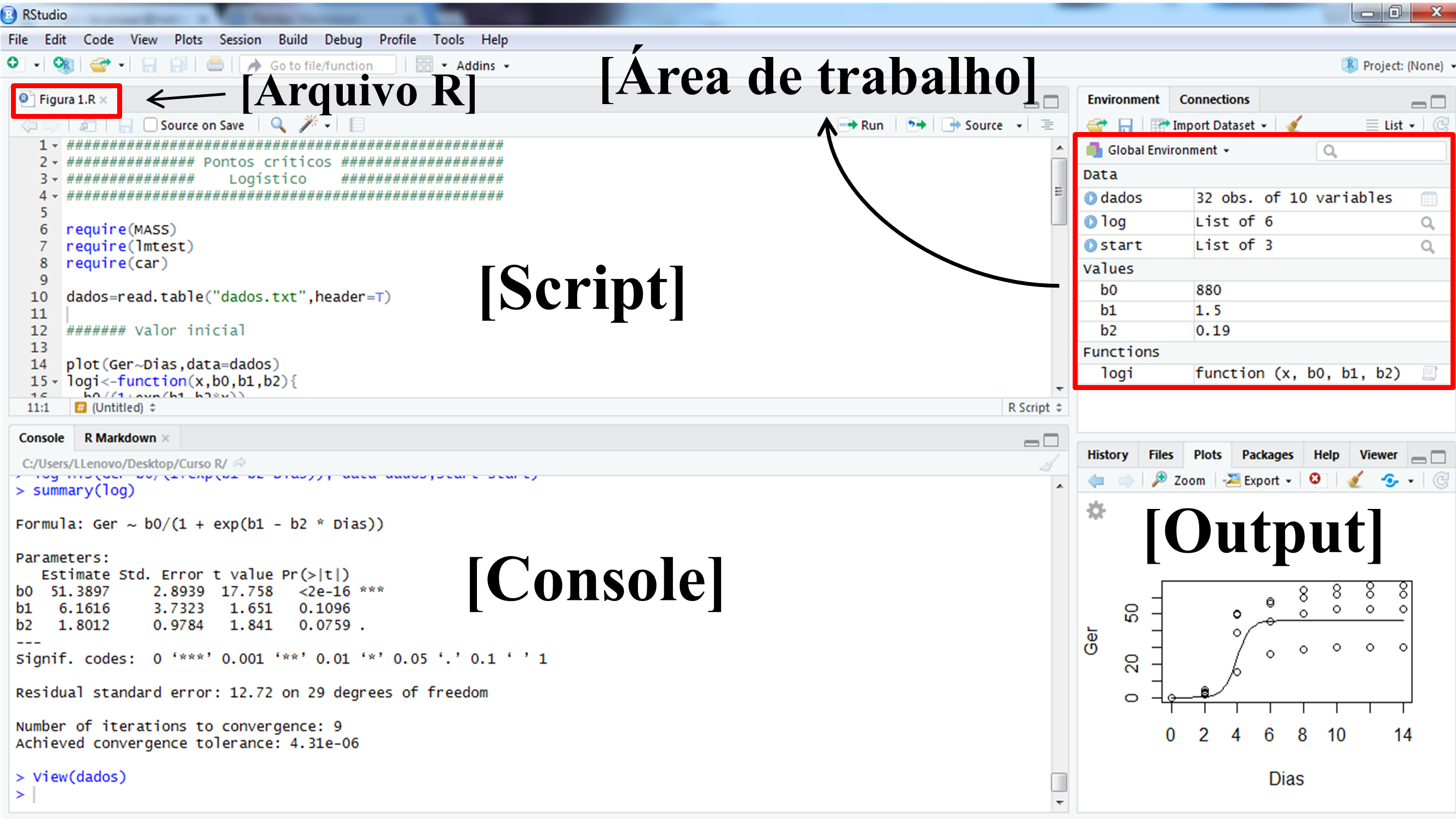
No canto inferior direito, além de servir como output para gráficos (Plots), também é o local onde os pacotes utilizados nas análises (Packages) são instalados e maiores informações sobre as funções podem ser encontradas (Help).
O primero passo é criar um novo script, seguindo os seguintes passos: File > New File > R script ou utilizando o atalho Ctrl+Shift+N. Para salvar um script, devemos clicar no botão com o símbolo de disquete (R/RStudio), escolher o nome do arquivo e o diretório onde o arquivo será armazenado no seu computador. Algumas importantes dicas:
Escolha sempre um nome sem caracteres especiais (ex., ç, ã, é, etc.)
Escolha sempre um nome curto ou abreviado, que identifique a finalidade das linhas de comando escritas (ex., dftese)
Evite espaços se o nome do arquivo for composto. Para isso, use um uderscore ‘_’(ex., df_tese)
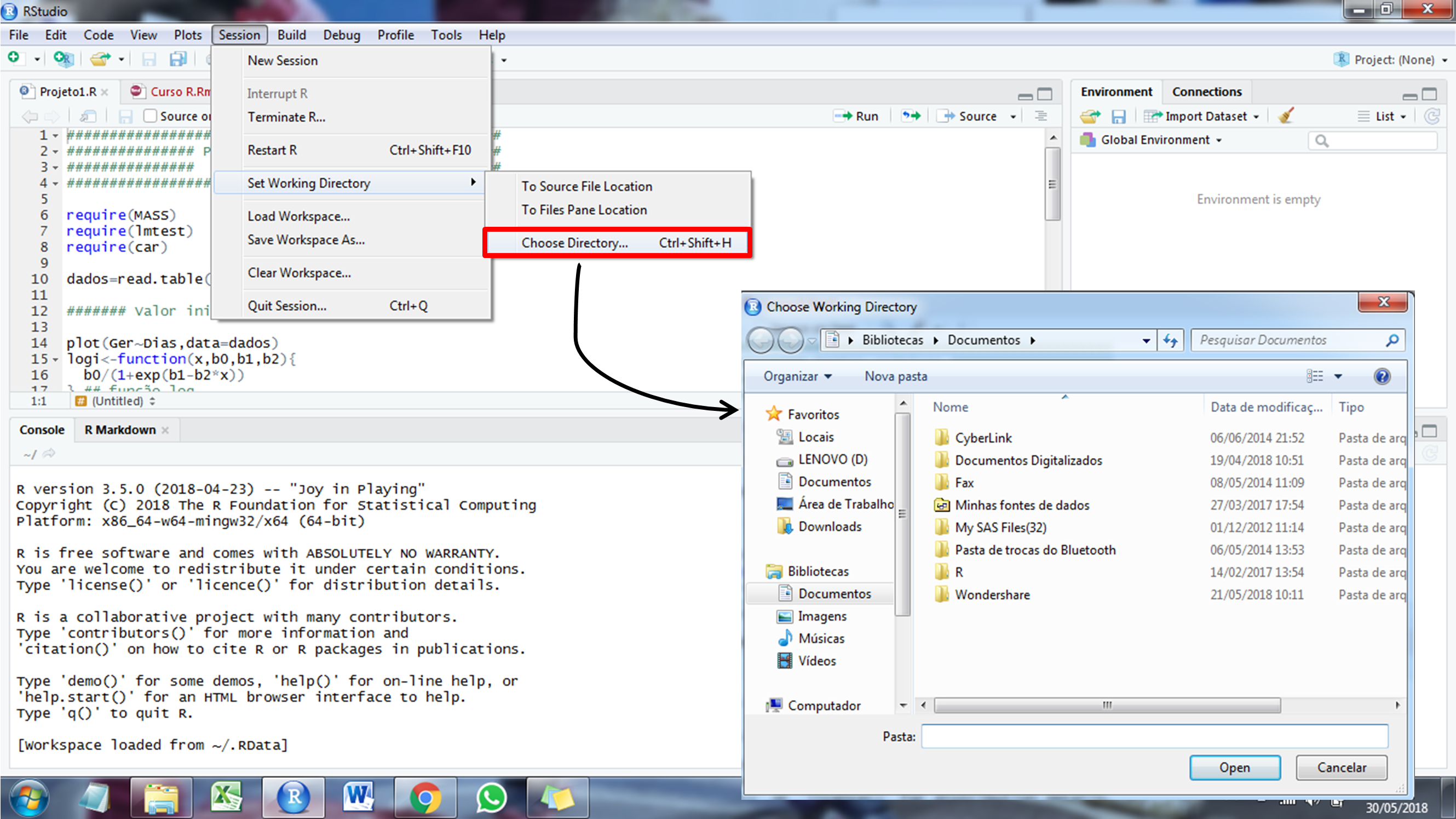
Antes de iniciar as análises, recomenda-se escolher um diretório onde devem estar os inputs (dados) e para onde serão enviados os outputs (gráficos, arquivos .txt, .xlsx, etc). Para selecionar o diretório, basta seguir o caminho Session > Set Working Directory > Choosing diretory ou utilizar as teclas de atalho Ctrl+Shift+H.
Se você realizou o download do software R pela primeira vez e achou um tanto quanto “estranho” o pequeno tamanho do arquivo (~80 Mb), provalemente deve ter se perguntado como um software estatistico tão poderoso pode ser comprimido em um arquivo tão pequeno (pequeno em comparação com os +20 GB do SAS). A resposta é simples: somente os pacote básicos do R são baixados com o arquivo de instalação. Na medida em que o usuário necessita realizar uma análise específica, a instalação de um pacote que contém uma função específica para realizar tal análise é necessária.
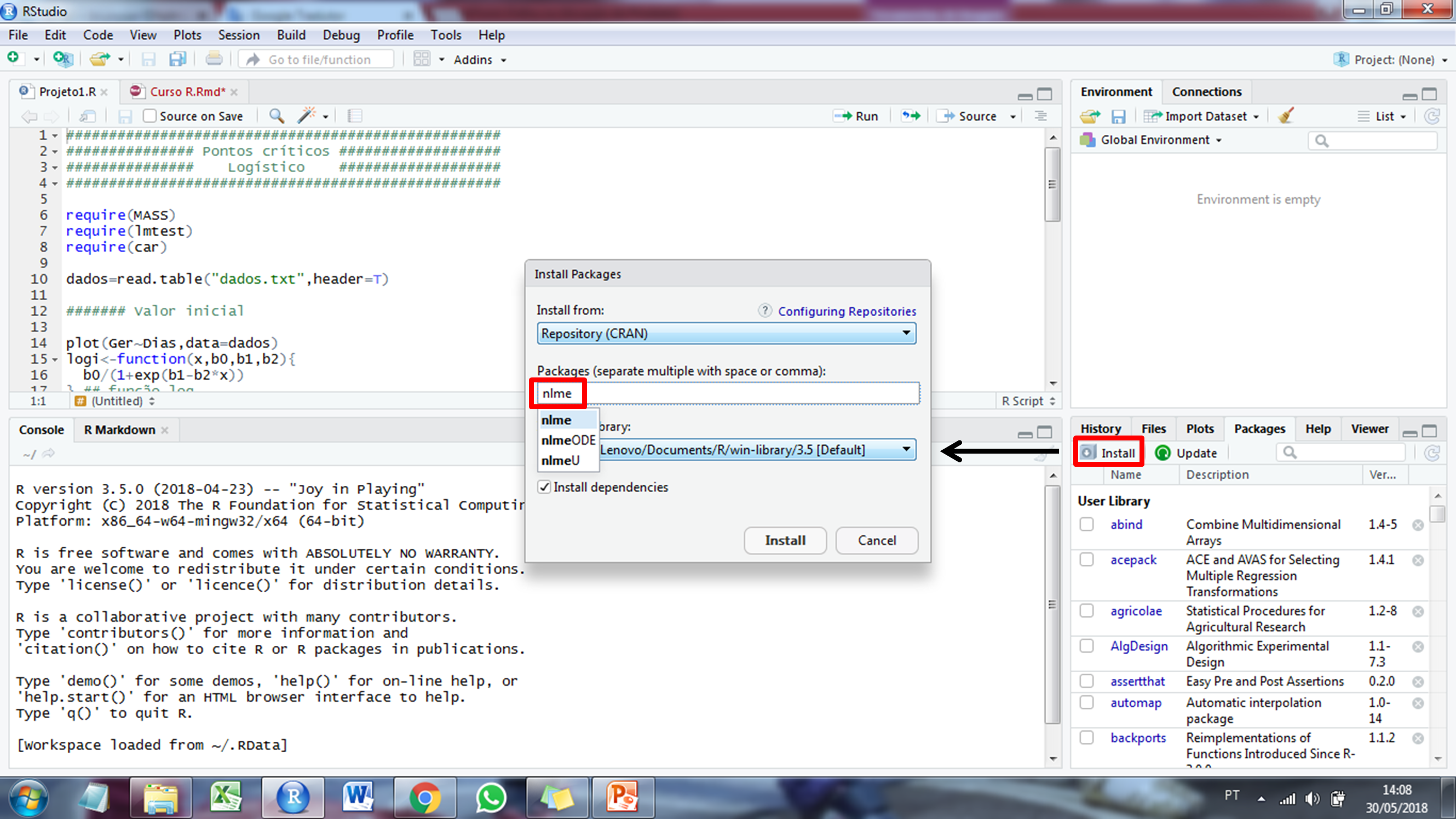
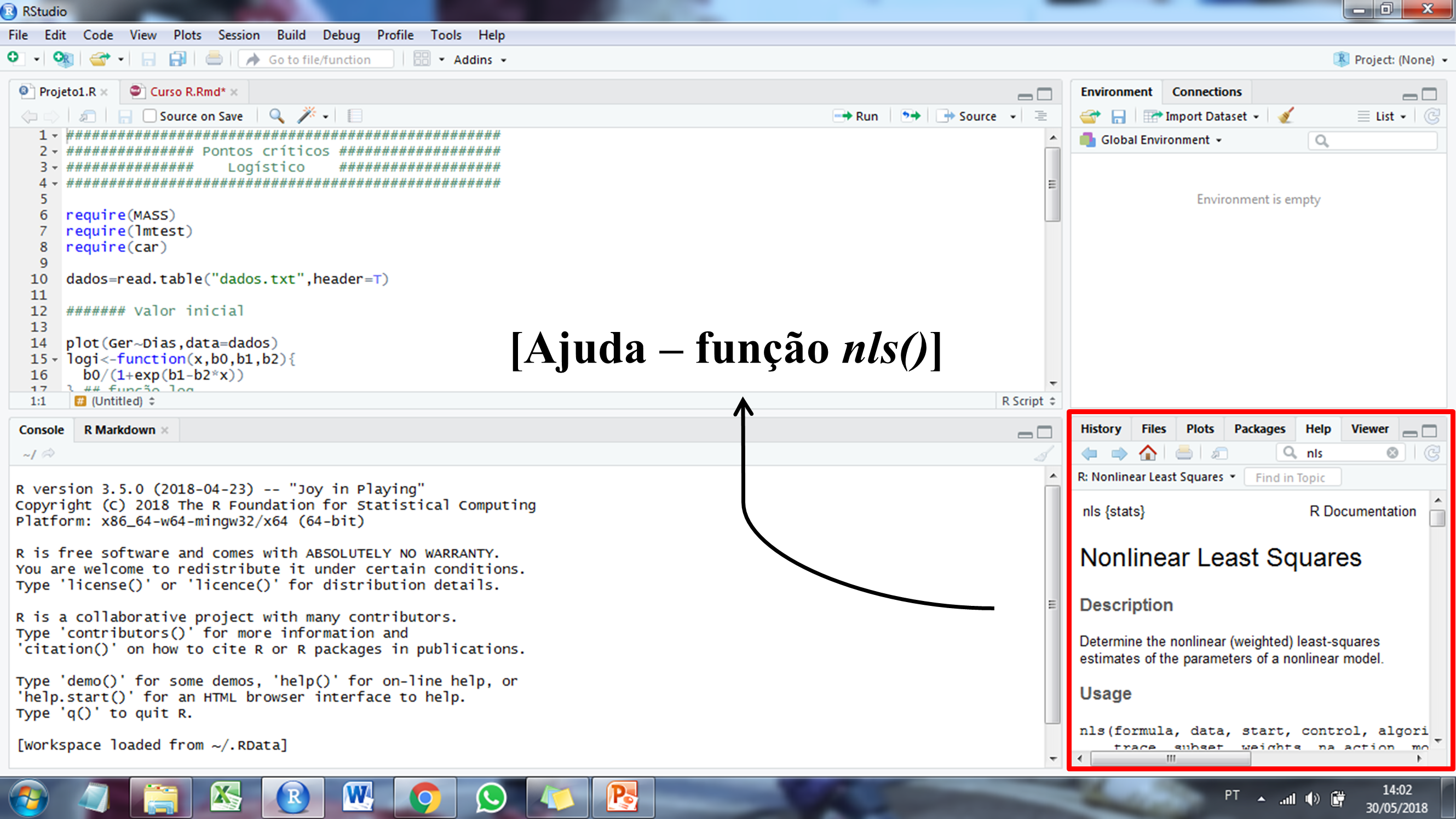
A instalação dos pacotes pode ser realizada conforme a figura abaixo, ou utilizando o comando install.packages(). Após a instalação do pacote, o usuário deve utilizar a função library() para que o pacote seja carregado e as suas funções possam ser utilizadas. Quando o usuário tenta utilizar uma função pertencente a um determinado pacote e este pacote não está instalado (ou carregado), um erro é exibido.
nls()Como exemplo inicial, vamos tentar selecionar a variável Sepal.Length do conjunto de dados base iris utilizando a função abaixo. Cuidado, spoilers do pacote dplyr!
Posteriormente, o seguinte código é digitado e executado ao se selecionar a linha do código e clicar no botão run ou utilizando o atalho Ctrl+Enter).
Error in select(iris, Sepal.Length): não foi possível encontrar a função "select"Neste caso, um erro é exibido pois o pacote dplyr não está instalado ou carregado. Caso ele já estiver instalado, a mensagem de erro acima é superada ao carregar o pacote antes de executar a função.
Caso o pacote dplyr não esteja instalado, a maneira mais fácil de instalá-lo é instalando a coleção de pacotes tidyverse7 seguindo os passos da Figura 3 ou utilizando a seguinte função.
O tidyverse é uma coleção de pacotes R projetados para a ciência de dados, contendo, dentre outros, seguintes pacotes que serão utilizados neste material.
Praticamente todas as rotinas realizadas no R são baseadas em bibliotecas de códigos. Para instalar os pacotes necessários para reprodução deste material, o seguinte código é utilizado.
É provável que a primeira instalação seja um pouco demorada, pois todas as dependências serão instaladas. Após finalizada a instalação, basta carregar o pacote que será utilizado com library().
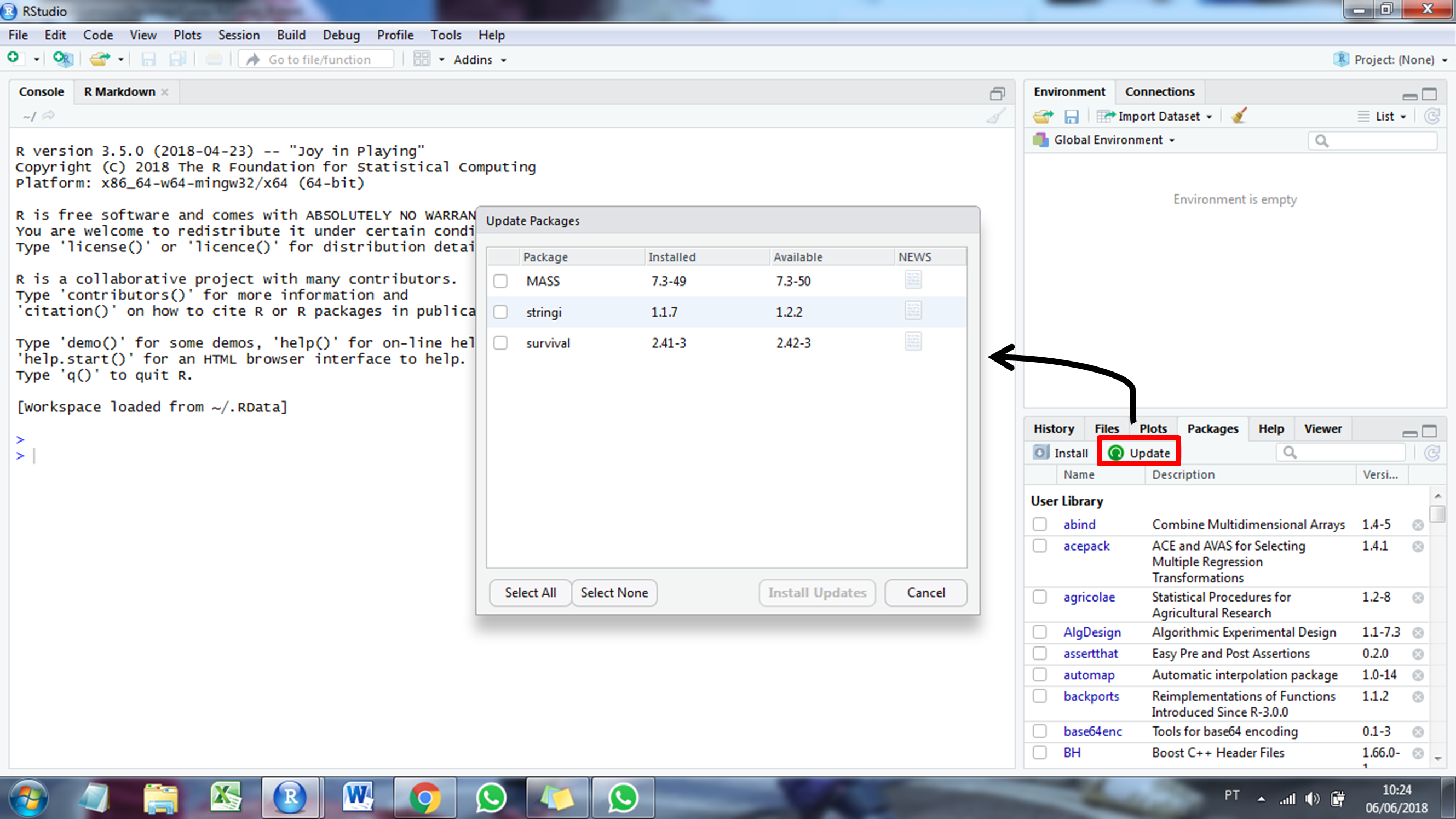
Os pacotes disponibilizados no software R estão em constante atualização. Para verificar novas versões de pacotes é possível ir em Packages > Update que se encontra no canto inferior direito conforme demonstrado na Figura 5.
Por fim, para citar os pacotes, recomenda-se verificar a referência através da função citation(). Para o pacote metan, por exemplo, a referência oficial é encontrada no artigo que descreve o pacote
Please, support this project by citing it in your publications!
Olivoto T, Lúcio AD (2020). "metan: An R package for
multi‐environment trial analysis." _Methods in Ecology and
Evolution_, *11*(6), 783-789. doi:10.1111/2041-210X.13384
<https://doi.org/10.1111/2041-210X.13384>.
Uma entrada BibTeX para usuários(as) de LaTeX é
@Article{,
title = {metan: An R package for multi‐environment trial analysis},
author = {Tiago Olivoto and Alessandro Dal’Col Lúcio},
year = {2020},
journal = {Methods in Ecology and Evolution},
volume = {11},
number = {6},
pages = {783-789},
doi = {10.1111/2041-210X.13384},
}Os comandos elementares podem ser divididos em expressões e atribuições. Por exemplo, podemos estar interessados em resolver a seguinte expressão \(10+15=25\).
No console quando passamos pelo comando, o R avalia a função e retorna o resultado. Caso queiramos armazenar este resultado em algum objeto, usamos a atribuição <- (Alt + -) que é utilizada no formato objeto <- operacao. Considerano o mesmo caso anterior, um objeto soma é criado com
Conhecendo estes comandos elementares, podemos passar para as operações matemáticas mais utilizadas e que são cruciais na linguagem de programação. No R, estas operações são baseadas em símbolos ou funções que se assemelham à maioria dos outros softwares estatísticos.
[1] 2[1] 1[1] 4[1] 9[1] 36[1] 2[1] 16[1] 2.302585[1] 2[1] 2.688117e+43Para multiplicação de matrizes utiliza-se %*% ao envéz de *. Note a diferença no exemplo abaixo.
[,1] [,2]
[1,] 1 3
[2,] 2 4 [,1] [,2]
[1,] 5 7
[2,] 6 8O resultado da multiplicação da matriz x e y é dado por:
\[ \left( {\begin{array}{*{20}{c}}{1 \cdot 5 + 3 \cdot 6}&{1 \cdot 7 + 3 \cdot 8}\\{2 \cdot 5 + 4 \cdot 6}&{2 \cdot 7 + 4 \cdot 8}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{23}&{31}\\{34}&{46}\end{array}} \right) \]
A função t() é utilizada para transposição de matrizes e solve() para inversão de matrizes. Vamos resolver o seguinte sistema de equações utilizando estes operadores.
\[ \begin{array}{l}{x_1} + 2{x_2} = 4\\{x_1} - {x_2} = 1\end{array} \]
Matricialmente o sistema acima é dado por:
\[ \left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}1\\1\end{array}}&{\begin{array}{*{20}{c}}2\\{ - 1}\end{array}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{x_1}}\\{{x_2}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}4\\1\end{array}} \right] \]
Esse sistema de equações é representado por \({\bf{AX}} = {\bf{c}}\) e tem como solução \({\bf{X = }}{{\bf{A}}^{{\bf{ - 1}}}}{\bf{c}}\)
[,1] [,2]
[1,] 1 2
[2,] 1 -1 [,1] [,2]
[1,] 1 1
[2,] 2 -1 [,1] [,2]
[1,] 0.3333333 0.6666667
[2,] 0.3333333 -0.3333333[1] 4 1 [,1]
[1,] 2
[2,] 1A função det() é utilizada para calcular o determinante de uma matriz e função eigen() para calcular calcular autovalores e autovetores
[,1] [,2] [,3]
[1,] 1 3 6
[2,] 2 4 1
[3,] 5 5 9[1] -68eigen() decomposition
$values
[1] 12.980067 2.854933 -1.835000
$vectors
[,1] [,2] [,3]
[1,] -0.4785227 0.2342735 -0.9165278
[2,] -0.2017392 -0.8386325 0.2624173
[3,] -0.8545861 0.4917432 0.3018507[1] 12.980067 2.854933 -1.835000 [,1] [,2] [,3]
[1,] -0.4785227 0.2342735 -0.9165278
[2,] -0.2017392 -0.8386325 0.2624173
[3,] -0.8545861 0.4917432 0.3018507A função diag() extrai a diagonal de uma matriz ou cria uma matriz onde a diagonal são os elementos declarados. Os próximos comandos extraem a diagonal de X e criam uma matriz identidade, com 3 linhas e 3 colunas.
https://www.jstor.org/stable/1390807?seq=1#page_scan_tab_contents↩︎
Fonte: Robert Gentleman<https://biocasia2020.bioconductor.org/>; Ross Ihaka: <https://stat.auckland.ac.nz/>↩︎
https://www.gnu.org/licenses/quick-guide-gplv3.html↩︎
https://www.r-project.org/↩︎
Veja uma breve história de como o pacote metan, desenvolvido pelo prof. Olivoto, foi concebido https://methodsblog.com/2020/05/28/metan_package/↩︎
https://www.rstudio.com/↩︎
https://www.tidyverse.org/↩︎
---
title: "1. O software R"
editor_options:
chunk_output_type: console
---
# O software R
O artigo [R: A Language for Data Analysis and Graphics](https://www.jstor.org/stable/1390807?seq=1#page_scan_tab_contents)[^1], escrito pelos desenvolvedores da linguagem George Ross Ihaka e Robert Clifford Gentleman, marca o início de uma nova era no processamento e análise de dados: o desenvolvimento do software R.
[^1]: https://www.jstor.org/stable/1390807?seq=1#page_scan_tab_contents
![Criadores do [^2]](figs/autores_r.png)
[^2]: Fonte: Robert Gentleman\<https://biocasia2020.bioconductor.org/\>; Ross Ihaka: \<https://stat.auckland.ac.nz/\>
[^3]: Fonte: Robert Gentleman\<https://biocasia2020.bioconductor.org/\>; Ross Ihaka: \<https://stat.auckland.ac.nz/\>
O R é uma linguagem e ambiente estatístico que traz muitas vantagens para o usuário, embora elas não sejam tão obvias inicialmente:
- O R é um Software Livre (livre no sentido de liberdade) distribuído sob a [Licença Pública Geral](https://www.gnu.org/licenses/quick-guide-gplv3.html)[^4], podendo ser livremente copiado, distribuído, e instalado em diversos computadores livremente. Isso contrasta com softwares comerciais, que têm licenças altamente restritivas, que não permitem que cópias sejam distribuídas ou instaladas em mais de um computador sem a devida licença (que obviamente é paga!);
- A grande maioria dos Softwares livres são grátis, e o R não é uma exceção;
- Os códigos-fontes R estão disponíveis para os usuários, e atualmente são gerenciados por um grupo chamado [R Development Core Team](https://www.r-project.org/)[^5]. A vantagem de ter o código aberto é que falhas podem ser detectadas e rapidamente corrigidas. Este sistema de revisão depende da participação dos usuários. Em contraste, em muitos pacotes comerciais, as falhas não são corrigidas até o lançamento da próxima versão, o que pode levar vários anos;
- O R fornece um interface de entrada por linha de comando (ELC).
[^4]: https://www.gnu.org/licenses/quick-guide-gplv3.html
[^5]: https://www.r-project.org/
No software R, todos os comandos são digitados e o mouse é pouco usado. Pode parecer antigo, pouco amigável ou até pobre em recursos visuais, mas isso faz com que nos deparemos com o melhor recurso do R: a sua flexibilidade. Para usuários familiarizados, a linguagem do R se torna clara e simples. Com poucos comandos, funções poderosas podem ser[^6] e o usuário é sempre consciente do que foi pedido através da ELC (Meus dados, minhas análises!). Isso contrasta com pacotes que possuem uma interface amigável (point-and-click), mas que escondem a dinâmica dos cálculos e, potencialmente, os seus erros. Finalmente, o R fornece uma ampla variedade de procedimentos estatísticos básicos ou que exigem grande esforço computacional (modelagem linear e não linear, testes estatísticos clássicos, análise de séries temporais, classificação, agrupamento, etc.) e recursos gráficos elegantes. Um dos pontos fortes de R é a facilidade com que gráficos de qualidade podem ser produzidos, incluindo símbolos matemáticos e fórmulas, quando necessário. O software R está disponível em uma ampla variedade de plataformas UNIX e sistemas similares (incluindo FreeBSD e Linux), Windows e MacOS.
[^6]: Veja uma breve história de como o pacote metan, desenvolvido pelo prof. Olivoto, foi concebido <https://methodsblog.com/2020/05/28/metan_package/>
# O software RStudio
Quem ja é usuário de softwares por linhas de comando, como o SAS, provavelmente não vai notar muita diferença. Toda análise se resume à seguinte sequência *dados \> códigos \> saída*. A experiência do usuário com o R, no entanto, pode ser mais atrativa utilizando o [RStudio](https://www.rstudio.com/)[^7]. O Rstudio é um produto de código aberto disponível publicamente em 28/02/2011 que está disponível gratuitamente. Ele é um ambiente de desenvolvimento integrado para R que inclui
[^7]: https://www.rstudio.com/
- Janelas de edição de texto a partir das quais o código pode ser enviado para o console e/ou salvo no sistema operacional
- Listas de objetos em sua área de trabalho
- Histórico infinito dos comandos facilmente pesquisável com capacidade de inserir, a partir do histórico, um comando no console novamente;
- Interface com o sistema operacional para acesso a arquivos;
- Janela de ajuda com botões de voltar e avançar
- Download de pacotes.
Nesta seção serão abordados alguns aspectos básicos para que o usuário do R possa desenvolver as suas análises. Será dado enfoque para áreas básicas da interface, cujo conhecimento é necessário para que um usuário inicante possa realizar sua primeira análisee. A figura abaixo mostra as principais janelas do **Rstudio**, incluindo o *script*, o *console*, a *"área de trabalho"* e o *output* para gráficos.

No canto inferior direito, além de servir como *output* para gráficos (*Plots*), também é o local onde os pacotes utilizados nas análises (*Packages*) são instalados e maiores informações sobre as funções podem ser encontradas (*Help*).
## Meu primeiro script
O primero passo é criar um novo script, seguindo os seguintes passos: *File \> New File \> R script* ou utilizando o atalho *Ctrl+Shift+N*. Para salvar um script, devemos clicar no botão com o símbolo de disquete (R/RStudio), escolher o nome do arquivo e o diretório onde o arquivo será armazenado no seu computador. Algumas importantes dicas:
- Escolha sempre um nome sem caracteres especiais (ex., ç, ã, é, etc.)
- Escolha sempre um nome curto ou abreviado, que identifique a finalidade das linhas de comando escritas (ex., dftese)
- Evite espaços se o nome do arquivo for composto. Para isso, use um uderscore '\_'(ex., df_tese)
## Diretório de trabalho
Antes de iniciar as análises, recomenda-se escolher um diretório onde devem estar os *inputs* (dados) e para onde serão enviados os *outputs* (gráficos, arquivos .txt, .xlsx, etc). Para selecionar o diretório, basta seguir o caminho *Session \> Set Working Directory \> Choosing diretory* ou utilizar as teclas de atalho *Ctrl+Shift+H*.

# Pacotes
Se você realizou o download do software R pela primeira vez e achou um tanto quanto "estranho" o pequeno tamanho do arquivo (\~80 Mb), provalemente deve ter se perguntado como um software estatistico tão poderoso pode ser comprimido em um arquivo tão pequeno (pequeno em comparação com os +20 GB do SAS). A resposta é simples: somente os pacote básicos do R são baixados com o arquivo de instalação. Na medida em que o usuário necessita realizar uma análise específica, a instalação de um pacote que contém uma função específica para realizar tal análise é necessária.
A instalação dos pacotes pode ser realizada conforme a figura abaixo, ou utilizando o comando `install.packages()`. Após a instalação do pacote, o usuário deve utilizar a função `library()` para que o pacote seja carregado e as suas funções possam ser utilizadas. Quando o usuário tenta utilizar uma função pertencente a um determinado pacote e este pacote não está instalado (ou carregado), um erro é exibido.


Como exemplo inicial, vamos tentar selecionar a variável *Sepal.Length* do conjunto de dados base `iris` utilizando a função abaixo. **Cuidado, spoilers do pacote dplyr!**
Posteriormente, o seguinte código é digitado e executado ao se selecionar a linha do código e clicar no botão *run* ou utilizando o atalho `Ctrl+Enter`).
```{r error=TRUE}
SL <- select(iris, Sepal.Length)
```
Neste caso, um erro é exibido pois o pacote **dplyr** não está instalado ou carregado. Caso ele já estiver instalado, a mensagem de erro acima é superada ao carregar o pacote antes de executar a função.
```{r eval=FALSE}
library(dplyr)
SL <- select(iris, Sepal.Length)
```
Caso o pacote **dplyr** não esteja instalado, a maneira mais fácil de instalá-lo é instalando a coleção de pacotes [tidyverse](https://www.tidyverse.org/)[^8] seguindo os passos da Figura 3 ou utilizando a seguinte função.
[^8]: https://www.tidyverse.org/
```{r eval=FALSE, message=FALSE, warning=FALSE}
install.packages("tidyverse", dependencies = TRUE)
library(tidyverse)
```
O **tidyverse** é uma coleção de pacotes R projetados para a ciência de dados, contendo, dentre outros, seguintes pacotes que serão utilizados neste material.
- **ggplot2**, para criação de gráficos.
- **dplyr**, para manipulação de dados.
- **tidyr**, para organização de dados.
- **tibble**, para criação de tibbles.
Praticamente todas as rotinas realizadas no R são baseadas em bibliotecas de códigos. Para instalar os pacotes necessários para reprodução deste material, o seguinte código é utilizado.
```{r, message=FALSE, warning=FALSE, eval=FALSE}
pacotes <- c("tidyverse", "esquisse", "metan", "rio")
# instalar os pacotes
install.packages(pacotes)
```
É provável que a primeira instalação seja um pouco demorada, pois todas as dependências serão instaladas. Após finalizada a instalação, basta carregar o pacote que será utilizado com `library()`.
```{r message=FALSE, warning=FALSE}
library(tidyverse)
```
Os pacotes disponibilizados no software *R* estão em constante atualização. Para verificar novas versões de pacotes é possível ir em *Packages \> Update* que se encontra no canto inferior direito conforme demonstrado na Figura 5.

Por fim, para citar os pacotes, recomenda-se verificar a referência através da função `citation()`. Para o pacote `metan`, por exemplo, a referência oficial é encontrada no [artigo](https://besjournals.onlinelibrary.wiley.com/doi/full/10.1111/2041-210X.13384) que descreve o pacote
```{r, echo = TRUE, eval = TRUE, message = FALSE, warning = FALSE, error = FALSE}
citation("metan")
```
# Comandos elementares
## Atribuições
Os **comandos elementares** podem ser divididos em **expressões** e **atribuições**. Por exemplo, podemos estar interessados em resolver a seguinte expressão $10+15=25$.
```{r}
10 + 15
```
No console quando passamos pelo comando, o R avalia a função e retorna o resultado. Caso queiramos armazenar este resultado em algum objeto, usamos a atribuição `<-` (Alt + -) que é utilizada no formato `objeto <- operacao`. Considerano o mesmo caso anterior, um objeto `soma` é criado com
```{r}
soma <- 10 + 15
```
## Operadores matemáticos
Conhecendo estes comandos elementares, podemos passar para as operações matemáticas mais utilizadas e que são cruciais na linguagem de programação. No R, estas operações são baseadas em símbolos ou funções que se assemelham à maioria dos outros softwares estatísticos.
```{r, echo = TRUE, message = FALSE, warning = FALSE}
1 + 1 # Soma
2 - 1 # Subtração
2 * 2 # Multiplicação
1 + 2 * 2 ^ 2 # Eleva ao quadrado, multiplica e soma
((1 + 2) * 2) ^ 2 # Soma, multiplica e eleva ao quadrado
sqrt(4) # Raiz quadrada
4^2 # Potência
log(10) # Por default, o logarítimo é de base e (logarítimo natural)
log(100, 10) # Logarítimo de base 10
exp(100) # exponencial
```
## Álgebra de matrizes (avançado)
Para multiplicação de matrizes utiliza-se `%*%` ao envéz de `*`. Note a diferença no exemplo abaixo.
```{r, message = FALSE, warning = FALSE}
(x <- matrix(1:4, ncol = 2))
(y <- matrix(5:8, ncol = 2))
```
O resultado da multiplicação da matriz `x` e `y` é dado por:
$$
\left( {\begin{array}{*{20}{c}}{1 \cdot 5 + 3 \cdot 6}&{1 \cdot 7 + 3 \cdot 8}\\{2 \cdot 5 + 4 \cdot 6}&{2 \cdot 7 + 4 \cdot 8}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{23}&{31}\\{34}&{46}\end{array}} \right)
$$
```{r, message = FALSE, warning = FALSE}
x * y # Errado
x %*% y # Certo
```
A função `t()` é utilizada para transposição de matrizes e `solve()` para inversão de matrizes. Vamos resolver o seguinte sistema de equações utilizando estes operadores.
$$
\begin{array}{l}{x_1} + 2{x_2} = 4\\{x_1} - {x_2} = 1\end{array}
$$
Matricialmente o sistema acima é dado por:
$$
\left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}1\\1\end{array}}&{\begin{array}{*{20}{c}}2\\{ - 1}\end{array}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{x_1}}\\{{x_2}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}4\\1\end{array}} \right]
$$
Esse sistema de equações é representado por ${\bf{AX}} = {\bf{c}}$ e tem como solução ${\bf{X = }}{{\bf{A}}^{{\bf{ - 1}}}}{\bf{c}}$
```{r echo = TRUE, eval = TRUE, message = FALSE, warning = FALSE}
(A <- matrix(c(1, 1, 2, -1), ncol = 2))
# Transposta de A
t(A)
# resolução do sistema de equações
(Ainv <- solve(A)) # Obtém a inversa generalizada de A
(c <- c(4, 1)) # Vetor C
(X <- Ainv %*% c)
```
::: callout-tip
Note que o mesmo resultado anterior pode ser obtido sem a necessidade de atribuição, ao declarar todas as operações em um único comando
```{r}
solve(matrix(c(1, 1, 2, -1), ncol = 2)) %*% c(4, 1)
```
:::
A função `det()` é utilizada para calcular o determinante de uma matriz e função `eigen()` para calcular calcular autovalores e autovetores
```{r echo = TRUE, eval = TRUE, message = FALSE, warning = FALSE}
(X <- matrix(c(1, 2, 5, 3, 4, 5, 6, 1, 9), ncol = 3))
(detX <- det(X))
```
```{r echo = TRUE, eval = TRUE, message = FALSE, warning = FALSE}
(av <- eigen(X))
av$values # Extrai os autovalores
```
```{r echo = TRUE, eval = TRUE, message = FALSE, warning = FALSE}
av$vectors # Extrai os autovetores
```
A função `diag()` extrai a diagonal de uma matriz ou cria uma matriz onde a diagonal são os elementos declarados. Os próximos comandos extraem a diagonal de X e criam uma matriz identidade, com 3 linhas e 3 colunas.
```{r echo = TRUE, eval = TRUE, message = FALSE, warning = FALSE}
diag(X)
diag(x = 1, nrow = 3, ncol = 3)
```
# Fóruns e materiais de apoio
::: {layout-ncol="3"}
[](https://www.youtube.com/watch?v=e89kyYJgWqc&list=PLJG9aEbqLtMiHWzBMBuakz33LtehOaUTD)
[](https://github.com/bendeivide/rapidinhasdor)
[](https://www.youtube.com/channel/UCDGyvLCJnv9RtTY1YMBMVNQ)
:::
# Homework
::: callout-important
## Meu primeiro relatório em R
- Utilizando o RStudio, crie um documento em formato quarto, salve em uma pasta de sua preferência.
- Neste relatório, apresente os comandos para instalação de dois pacotes que acreditas serem de utilidade em sua área de estudo.
- Descreva brevemente os pacotes instalados
:::
{{< video https://www.youtube.com/embed/MO9jPS1xZdQ >}}
```{=html}
<div align='center'><a href='https://www.free-website-hit-counter.com'><img src='https://www.free-website-hit-counter.com/c.php?d=9&id=138588&s=2' border='0' alt='Free Website Hit Counter'></a><br / ><small><a href='https://www.free-website-hit-counter.com' title="Free Website Hit Counter">Free website hit counter</a></small></div>
```